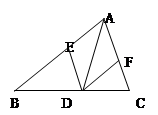如图，一次函数y1＝k1x＋2与反比例函数y2＝
的图象交于点A (4，m)和B(－8，－2)，与y轴交于点C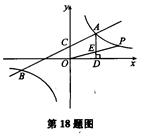
k1＝_______，k2＝______
根据函数图象可知，当y1>y2时，x的取值范围是______．
过点A作AD⊥x轴于点D，点P是反比例函数在第一象限的图象上一点．设直线OP与线段AD交于点E，当S四边形ODAC：S△CE＝3：1时，求点P的坐标
如图：在平面直角坐标系中A(2，6),B(-1，1)，C(4，3).在下图中作出 △ABC关于y轴对称图形△A1B1C1.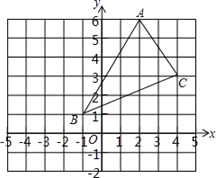
如图，△ABC中，AB=AC，AE是外角∠CAD的平分线，求证：AE∥BC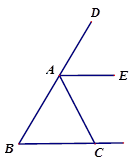
在△ABC中，∠B=∠A+20O，∠C=∠B+20O，求△ABC的三个内角的度数.
已知△ABC中，∠ABC=90゜，AB=BC，点A、B分别是x轴和y轴上的一动点．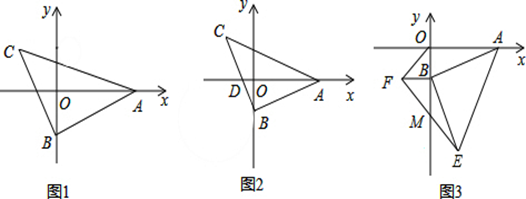
（1）如图1，若点C的横坐标为4，求点B的坐标；
（2）如图2，BC交x轴于D，AD平分∠BAC，若点C的纵坐标为3，A（5，0），求点D的坐标．
（3）如图3，分别以OB、AB为直角边在第三、四象限作等腰直角△OBF和等腰直角△ABE，EF交y轴于M，求S△BEM：S△ABO．
如图，已知AD是△ABC的角平分线，在不添加任何辅助线的前提下，要使△AED≌△AFD，需添加一个条件是：_______________，并给予证明.