如图,在直角坐标系中, 是原点,
是原点, 三点的坐标分别
三点的坐标分别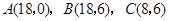 ,四边形
,四边形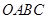 是梯形,点
是梯形,点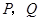 同时从原点出发,分别作匀速运动,其中点
同时从原点出发,分别作匀速运动,其中点 沿
沿 向终点
向终点 运动,速度为每秒
运动,速度为每秒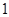 个单位,点
个单位,点 沿
沿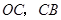 向终点
向终点 运动,当这两点有一点到达自己的终点时,另一点也停止运动.
运动,当这两点有一点到达自己的终点时,另一点也停止运动.
(1)求直线 的解析式.
的解析式.
(2)设从出发起,运动了 秒.如果点
秒.如果点 的速度为每秒
的速度为每秒 个单位,试写出点
个单位,试写出点 的坐标,并写出此时
的坐标,并写出此时 的取值范围.
的取值范围.
(3)设从出发起,运动了 秒.当
秒.当 ,
, 两点运动的路程之和恰好等于梯形
两点运动的路程之和恰好等于梯形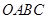 的周长的一半,这时,直线
的周长的一半,这时,直线 能否把梯形的面积也分成相等的两部分,如有可能,请求出
能否把梯形的面积也分成相等的两部分,如有可能,请求出 的值;如不可能,请说明理由.
的值;如不可能,请说明理由.
(自贡)观察下表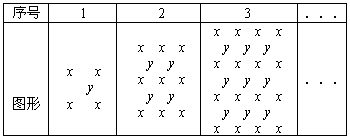
我们把某格中字母和所得的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y,回答下列问题:
(1)第3格的“特征多项式”为 ,第4格的“特征多项式”为 ,第n格的“特征多项式”为 ;
(2)若第1格的“特征多项式”的值为-10,第2格的“特征多项式”的值为-16,
①求x,y的值;
②在此条件下,第n格的特征是否有最小值?若有,求出最小值和相应的n值,若没有,说明理由.
(内江)(1)填空: = ;
= ;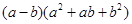 = ;
= ;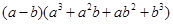 = .
= .
(2)猜想: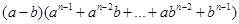 = (其中n为正整数,且
= (其中n为正整数,且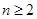 ).
).
(3)利用(2)猜想的结论计算: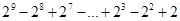 .
.
(达州)在△ABC的外接圆⊙O中,△ABC的外角平分线CD交⊙O于点D,F为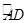 上一点,且
上一点,且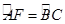 连接DF,并延长DF交BA的延长线于点E.
连接DF,并延长DF交BA的延长线于点E.
(1)判断DB与DA的数量关系,并说明理由;
(2)求证:△BCD≌△AFD;
(3)若∠ACM=120°,⊙O的半径为5,DC=6,求DE的长.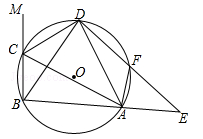
(南充)已知关于x的一元二次方程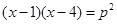 ,p为实数.
,p为实数.
(1)求证:方程有两个不相等的实数根;
(2)p为何值时,方程有整数解.(直接写出三个,不需说明理由)
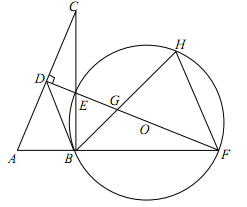
(成都)(本小题满分10分)如图,在Rt△ABC中,∠ABC=90°,AC的垂直平分线分别与AC,BC及AB的延长线相交于点D,E,F,且BF=BC.⊙O是△BEF的外接圆,∠EBF的平分线交EF于点G,交于点H,连接BD、FH.
(1)求证:△ABC≌△EBF;
(2)试判断BD与⊙O的位置关系,并说明理由;
(3)若AB=1,求HG•HB的值.