某批发商以每件50元的价格购进800件T恤．第一个月以单价80元销售，售出了200件；第二个月如果单价不变，预计仍可售出200件，批发商为增加销售量，决定降价销售，根据市场调查，单价每降低1元，可多售出10件，但最低单位应高于购进的价格；第二个月结束后，批发商将对剩余的T恤一次性清仓销售，清仓时单价为40元．设第二个月单价降低x元．
（1）填表(不需要化简)
| 时间 |
第一个月 |
第二个月 |
清仓时 |
| 单价(元) |
80 |
▲ |
40 |
| 销售量(件) |
200 |
▲ |
▲ |
（2）如果批发商希望通过销售这批T恤获利9000元，那么第二个月的单价应是多少元？
已知关于x的方程x2－2（k－1）x+ k2=0有两个实数根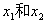
（1）求k的取值范围；
（2）若
，求k的值.
在一个不透明的盒子里，装有四个分别标有数字1，2，3，4的小球，它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球，记下数字为x；放回盒子摇匀后，再由小华随机取出一个小球，记下数字为y.
（1）用列表法或画树状图表示出（x，y）的所有可能出现的结果；
（2）求小明、小华各取一次小球所确定的点（x，y）落在反比例函数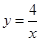
的图象上的概率；
（3）求小明、小华各取一次小球所确定的数x、y满足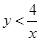
的概率.
某校初三课外活动小组，在测量树高的一次活动中，如图7所示，测得树底部中心A到斜坡底C的水平距离为8. 8m．在阳光下某一时刻测得1米的标杆影长为0.8m，树影落在斜坡上的部分CD= 3.2m．已知斜坡CD的坡比i=1：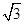
，求树高AB。（结果保留整数，参考数据：
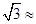1.7）
益趣玩具店购进一种儿童玩具，计划每个售价36元，能盈利80﹪，在销售中出现了滞销，于
是先后两次降价，售价降为25元。
（1）求这种玩具的进价。
（2）求平均每次降价的百分率（精确到0.1﹪）。
如图，△ABC中， BE⊥AC于E,AD⊥BC于D.求证：△CDE∽ △CAB