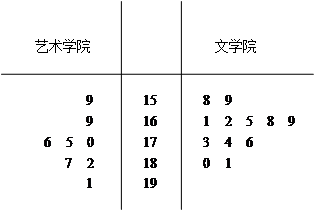
为把中国武汉大学办成开放式大学，今年樱花节武汉大学在其属下的艺术学院和文学院分别招募8名和12名志愿者从事兼职导游工作，将这20志愿者的身高编成如下茎叶图（单位：厘米）若身高在175cm及其以上定义为“高个子”，否则定义为“非高个子”且只有文学院的“高个子”才能担任兼职导游。
（1）根据志愿者的身高茎叶图指出文学院志愿者身高的中位数
（2）如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人，再从这5人中选2人，那么至少有一人是“高个子”的概率是多少
（3）若从所有“高个子”中选3名志愿者。用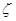
表示所选志愿者中能担任“兼职导游”的人数，试写出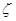的分布列，并求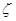的数学期望
(
cos
,
sin
=" (" – sin
,cos
，求向量
中，内角
的对边分别是
，已知
．
求角B的大小．
中
，
，
．
中
，
，
，
的左、右焦点分别为
，
．过
两点，过
两点，且
，垂足为
．
，证明：
；
的面积的最小值．
．
的导数
；
都有
，求
的取值范围．