解分式方程: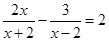
如图,已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连接QE并延长交BP于点F.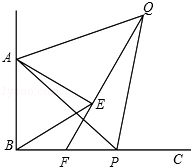
(1)试说明:∠AEQ=90°;
(2)猜想EF与图中哪条线段相等(不能添加辅助线产生新的线段),并说明理由.
如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
求证:(1)∠ECD=∠EDC;
(2)OC=OD;
(3)OE是线段CD的垂直平分线.
如图,已知四边形ABCD是梯形,AD∥BC,∠A=90°,BC=BD,CE⊥BD,垂足为E.
(1)求证:△ABD≌△ECB;
(2)若∠DBC=50°,求∠DCE的度数.
观察下列各式:
3×5=15=42﹣1
5×7=35=62﹣1
11×13=143=122﹣1
…
根据你的观察、归纳、猜想,请将你发现的规律,用只含一个字母n的式子表示出来,并予以证明.
先化简再求值( +
+ )÷
)÷ ,其中m=
,其中m= .
.