某商场家电销售部有营业员20名,为了调动营业员的积极性,决定实行目标管理,即确定一个月的销售额目标,根据目标完成情况对营业员进行适当的奖惩.为此,商场统计了这20名营业员在某月的销售额,数据如下:(单位:万元)
25 26 21 17 28 26 20 25 26 30
20 21 20 26 30 25 21 19 28 26
(1)请根据以上信息完成下表:
| 销售额(万元) |
17 |
19 |
20 |
21 |
25 |
26 |
28 |
30 |
| 频数(人数) |
1 |
1 |
3 |
3 |
|
|
2 |
2 |
(2)上述数据中,众数是 万元,中位数是 万元,平均数是 万元;
(3)如果将众数作为月销售额目标,能否让至少一半的营业员都能达到目标?请说明理由.
当a=-3,b=-2,c=5时,求下列各代数式的值。
(1)a÷bc(即a÷(bc));
(2)ab÷c;
(3)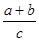 ;
;
(4)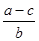 ;
;
(5)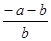 ;
;
(6)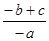 ;
;
某包装盒的展开图,尺寸如图所示(单位:cm)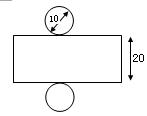
(1)这个几何体的名称是;
(2)求这个包装盒的表面积
如图,已知AB=CD,∠B=∠C,AC和BD交于点O,E是AD的中点,连接OE.
(1)求证:△AOD≌△DOC;
(2)求∠AEO的度数.
小华爸爸上星期五买进某公司股票1000股,每股27元,下表为本周内每日该股票的涨跌情况。(单位:元)
| 星期 |
一 |
二 |
三 |
四 |
五 |
| 每股涨跌 |
+4 |
-1 |
-2.5 |
+4.5 |
-6 |
(1)通过上表你认为星期三收盘时,每股是多少元?
(2)本周内每股最高是多少元?最低是多少元?
(3)已知小华爸爸买进股票时付了千分之3的手续费,卖出时因优惠免手续费但要交成交额千分之2的交易税,如果小华爸爸在星期五收盘前将全部股票卖出,他的收益情况如何?
计算: .
.