某开发区为改善居民住房条件，每年都新建一批住房，人均住房面积逐年增加[人均住房面积=（该区住房总面积/该区人口总数）（单位：m2/人）]，该开发区2004年至2006年每年年底人均住房面积和人口总数的统计如图1，图2．
请根据图1，图2提供的信息解答下面问题：（1）该区2005年和2006年两年中哪一年比上一年增加的住房面积多？多增加多少平方米？
（2）由于经济发展需要，预计到2008年底该区人口总数比2006年底增加2万人，为使到2008年底该区人均住房面积达到11m2/人，试求2007年和2008年这两年该区住房总面积的年平均增长率为多少
数学实验室：（本题12分）
点A、B在数轴上分别表示有理数a、b，A、B两点之间的距离表示为AB，在数轴上A、B两点之间的距离AB=|a-b|．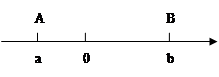
利用数形结合思想回答下列问题：
①数轴上表示2和5两点之间的距离是________,数轴上表示1和﹣3的两点之间的距离是________．(2分)
②数轴上表示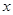
和
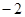的两点之间的距离表示为__________．(3分)
③若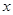表示一个有理数，且
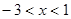，化简：
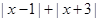(4分)
④若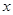表示一个有理数，且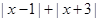＞4，则有理数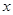的取值范围是___________________(3分)
（本题10分）2013年第23号台风“菲特”给浙江省带来了严重的影响。强降雨导致多处河水猛涨，城区受淹。西湖也出现了罕见的水满现象。在10月7日凌晨，西湖达到警戒水位7．3 m ．下表记录了这几日西湖水位的变化情况：（把10月7日凌晨的水位记作0，此后，正数表示比前一观察时间上升，负数表示下降）。
| 时间 |
10月7日凌晨 |
10月7日15时 |
10月8日、 |
10月9日 8时 |
10月10日12时 |
10月10日15点 |
| 水位变化 （米） |
0 |
+0．15 |
+0．20 |
-0．13 |
-0．26 |
-0．03 |
（1）10月9日8时西湖水位是多少？
（2）这几日西湖水位最高值是多少？超过警戒水位多少米？
（3）从表中可以得知什么时候开始西湖水位已恢复到警戒水位之下？
（本题8分）已知|x|=3，（y+1）2=4，且xy＜0，求x-y的值．
（本题8分）规定△是一种新的运算符号，且a△b=a2-a×b+a-1，例如：计算2△3=22-2×3+2-1=4-6+2-1=-1．请你根据上面的规定试求
（1）4△5（2）﹣3△4
（本题8分）已知a、b互为相反数，m、n互为倒数，x 绝对值为2，求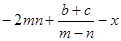
的值．