如图a，△ABC和△CEF是两个大小不等的等边三角形（等边三角形为三条边相等，三个角为60°的三角形），且有一个公共顶点C，点F、B、C在同一直线上，连结AF和BE。
(1)线段AF和BE有怎样的大小关系?（写出结论，不需要说明理由）
(2)将图a中的△CEF绕点C旋转一定的角度，得到图b，(1)中的结论还成立吗?作出判断并说明理由；
如图矩形ABCD中，过A，B两点的⊙O切CD于E，交BC于F，AH⊥BE于H，连结EF。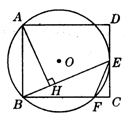
⑴求证：∠CEF＝∠BAH,⑵若BC＝2CE＝6，求BF的长。
现有两个纸箱,每个纸箱内各装有4个材质、大小都相同的乒乓球,其中一个纸箱内4个小球上分别写有1、2、3、4这4个数，另一个纸箱内4个小球上分别写有5、6、7、8这4个数，甲、乙两人商定了一个游戏，规则是：从这两个纸箱中各随机摸出一个小球，然后把两个小球上的数字相乘，若得到的积是2的倍数，则甲得1分，若得到积是3的倍数，则乙得2分.完成一次游戏后,将球分别放回各自的纸箱,摇匀后进行下一次游戏,最后得分高者胜出.。
(1)请你通过列表(或树状图)分别计算乘积是2的倍数和3的倍数的概率;
(2)你认为这个游戏公平吗?为什么?若你认为不公平,请你修改得分规则,使游戏对双方公平.
（1）计算：2sin60°－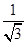
＋(
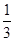)－1＋(－1)2008
（2）解方程：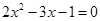
实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等。（共10分）
(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b反射出的光线n与光线m平行,且∠1=38°,则∠2=°,∠3=°。
(2)在(1)中,若∠1=55°,则∠3=°;若∠1=40°,则∠3=°。
(3)由(1)、(2),请你猜想:当两平面镜a、b的夹角∠3=°时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行.你能说明理由吗?
从一个五边形中切去一个三角形，得到一个三角形和一个新的多边形，那么这个新的多边形的内角和等于多少度？请画图说明．