某土产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售．按计划20辆车都要装运，每辆汽车只能装运同一种土特产，且必须装满．根据下表提供的信息，解答以下问题：
| 土特产种类 |
甲 |
乙 |
丙 |
| 每辆汽车运载量（吨） |
8 |
6 |
5 |
| 每吨土特产获利（百元） |
12 |
16 |
10 |
设装运甲种土特产的车辆数为
，装运乙种土特产的车辆数为
，求与之间的函数关系式如果装运每种土特产的车辆都不少于3辆，那么车辆的安排方案有几种？并写出每种安排方案．
若要使此次销售获利最大，应采用（2）中哪种安排方案？并求出最大利润的值
计算：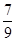
×｛
[2×(-1)3-7]-18｝-（3×
）2
用简便方法计算：（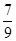
-
+
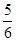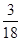）×18-1.45×6+3.95×6
请画一个数轴，在数轴上表示下列各数，并用“<”把这些数连起来：3、-2、0、-
、2.5.
试用两种不同的方法对下列有理数分类：0、-3、
、-
、0.24、5
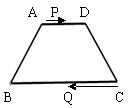
如图，在等腰梯形ABCD中，AD∥BC，AB=DC=5，AD=6，BC=12，动点P从A点出发以每秒1个单位的速度向终点D运动，动点Q从C点出发以每秒2个单位的速度向终点B运动，两点同时出发，设运动时间为t.
（1）梯形ABCD的面积是。
（2）①当t为多少秒时，四边形ABQP是平行四边形？
②当t为多少秒时，四边形ABQP是梯形？
（3）当t=3秒时通过计算判断四边形ABQP是否是直角梯形？