⑴ 解方程: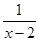 =
=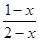 -3⑵ 解不等式组:
-3⑵ 解不等式组: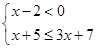
计算:(1)(-3)2- +(-1)0+
+(-1)0+
(2)
如图,已知二次函数y=a(x2-6x+8)(a>0)的图象与x轴交于点A、B两点,与y轴交于点C.
(1)求A、B两点的坐标;
(2)若S△ABC=8,则过A、B、C三点的圆是否与抛物线有第四个交点D?若存在,求出D点坐标;若不存在,说明理由.
(3)将△OAC沿直线AC翻折,点O的对应点为O'.
①若O'落在该抛物线的对称轴上,求实数a的值;
②是否存在正整数a,使得点O'落在△ABC的内部,若存在,求出整数a的值;若不存在,请说明理由.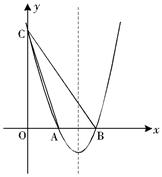
如图,在平面直角坐标中,点A的坐标为(1,1),OA=AC,∠OAC=90°,点D为x轴上一动点.以AD为边在AD的右侧作正方形ADEF.
(1)当点D在线段OC上时(不与点O、C重合),则线段CF与OD之间的数量关系为;位置关系为,
(2)当点D在线段OC的延长线上时,(1)中的结论是否成立?若成立,请说明理由;若不成立,请举一反例;
(3)设D点坐标为(t,0),当D点从O点运动到C点时,用含t的代数式表示E点坐标,并直接写出E点所经过的路径长.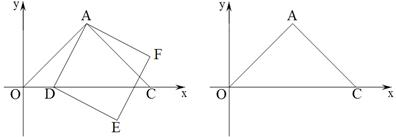
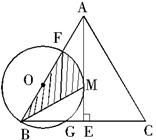
如图△ABC中,AB=AC,AE⊥BC,E为垂足,F为AB上一点.以BF为直径的圆与AE相切于M点,交BC于G点.
(1)求证:BM平分∠ABC;
(2)当BC=4,cosC= 时,
时,
①求⊙O的半径;
②求图中阴影部分的面积.(结果保留π与根号)