如图，在平面直角坐标中，点A的坐标为（1，1），OA=AC，∠OAC=90°，点D为x轴上一动点．以AD为边在AD的右侧作正方形ADEF．
（1）当点D在线段OC上时（不与点O、C重合），则线段CF与OD之间的数量关系为 ；位置关系为 ，
（2）当点D在线段OC的延长线上时，（1）中的结论是否成立？若成立，请说明理由；若不成立，请举一反例；
（3）设D点坐标为（t，0），当D点从O点运动到C点时，用含t的代数式表示E点坐标，并直接写出E点所经过的路径长．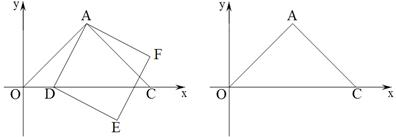
下图是单位长度为1的正方形网格，点A、B、C都在格点上；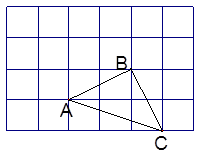
（1）画出将图中的△ABC绕点A逆时针旋转90°的△AB’C’ ，（其中B、C的对应点分别是
B’、C’）
（2）求（1）中点B在运动过程中所经过的弧长．
（3）求（1）中边AC在运动过程中所扫过的区域的面积．
如图，纸片ABCD是一个菱形，其边长为2，∠BAD＝120°，以点A为圆心的扇形与边BC相切于点E，与AB、AD分别相交于点F、G；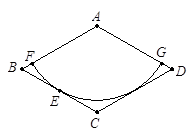
（1）请你判断所作的扇形与边CD的位置关系，并说明理由；
（2）若以所作出的扇形为侧面围成一个圆锥，求该圆锥的全面积．
已知关于x的一元二次方程x2 + mx +n+1=0的一根为2．
（1）用m的代数式表示n；
（2）求证：关于y的一元二次方程y2 +my+n=0总有两个不相等的实数根。
如图，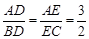
，试求
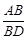和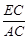
的值．（4+4）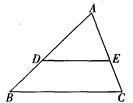
先化简，再求值：
，其中a满足方程a2+4a+1=0．