如图,在边长为1个单位长度的小正方形组成的网格中,按要求画出△A1B1C1和△A2B2C2;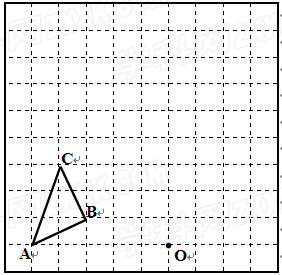
(1)将△ABC向右平移4个单位,再向上平移1个单位,得到△A1B1C1;
(2)以图中的O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2.
如图,等边三角形ABC的边长为4,直线l经过点A并与AC垂直.当点P在直线l上运动到某一位置(点P不与点A重合)时,连接PC,并将△ACP绕点C按逆时针方向旋转 得到△BCQ,记点P的对应点为Q,线段PA的长为m(
得到△BCQ,记点P的对应点为Q,线段PA的长为m( ).
).
(1)①∠QBC= ;
;
② 如图1,当点P与点B在直线AC的同侧,且 时,点Q到直线l的距离等于;
时,点Q到直线l的距离等于;
(2)当旋转后的点Q恰好落在直线l上时,点P,Q的位置分别记为 ,
, .在图2中画出此时的线段
.在图2中画出此时的线段 及△
及△ ,并直接写出相应m的值;
,并直接写出相应m的值;
(3)当点P与点B在直线AC的异侧,且△PAQ的面积等于 时,求m的值.
时,求m的值.
如图,在平面直角坐标系xOy中,点 ,
, 在反比例函数
在反比例函数 (m为常数)的图象G上,连接AO并延长与图象G的另一个交点为点C,过点A的直线l与x轴的交点为点
(m为常数)的图象G上,连接AO并延长与图象G的另一个交点为点C,过点A的直线l与x轴的交点为点 ,过点C作CE∥x轴交直线l于点E.
,过点C作CE∥x轴交直线l于点E.
(1)求m的值及直线l对应的函数表达式;
(2)求点E的坐标;
(3)求证:∠BAE=∠ACB.
已知抛物线C: .
.
(1)补全表中A,B两点的坐标,并在所给的平面直角坐标系中画出抛物线C;
(2)将抛物线C上每一点的横坐标变为原来的2倍,纵坐标变为原来的 ,可证明得到的曲线仍是抛物线,(记为
,可证明得到的曲线仍是抛物线,(记为 ),且抛物线
),且抛物线 的顶点是抛物线C的顶点的对应点,求抛物线
的顶点是抛物线C的顶点的对应点,求抛物线 对应的函数表达式.
对应的函数表达式.
如图,在⊙O中,弦BC,BD关于直径AB所在直线对称.E为半径OC上一点,OC=3OE,连接AE并延长交⊙O于点F,连接DF交BC于点M.
(1)请依题意补全图形;
(2)求证:∠AOC=∠DBC;
(3)求 的值.
的值.
如图,在正方形ABCD中,有一个小正方形EFGH,其中顶点E,F,G分别在AB,BC,FD上.
(1)求证:△EBF∽△FCD;
(2)连接DH,如果BC=12,BF=3,求tan∠HDG的值.