(1)阅读理解
先观察和计算,并用“>”、“<”、“≥”、“≤”、“=”填空:4+9 2 ,
,
4+4 2 ,2+3 2
,2+3 2 。请猜想:当
。请猜想:当 则
则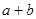
 。
。
如∵ 展开
展开 ∴6+5
∴6+5 。
。
请你给出猜想的一个相仿的说明过程。
(2)知识应用
①如图⊙O中,⊙O的半径为5,点P为⊙O内一个定点,OP=2,过点P作两条互相垂直的弦,即AC⊥BD, 作ON⊥BD,OM⊥AC,垂足为M、N,求 的值。
的值。
②在上述基础上,连接AB、BC、CD、DA,利用①中的结论,探求四边形ABCD面积的最大值。
(本小题满分5分)
已知:如图,AB是⊙O的直径,CD是⊙O的弦,且AB⊥CD,垂足为E,联结OC, OC=5.
(1)若CD=8,求BE的长;
(2)若∠AOC=150°,求扇形OAC的面积.
(本小题满分5分)
已知二次函数 .
.
(1)将 化成y=a (x-h) 2 +k的形式;
化成y=a (x-h) 2 +k的形式;
(2)指出该二次函数图象的对称轴和顶点坐标;
(3)当x取何值时,y随x的增大而增大?
(本小题满分5分)
已知:如图,在 中,D是AC上一点,联结BD,且∠ABD =∠ACB.
中,D是AC上一点,联结BD,且∠ABD =∠ACB.
(1)求证:△ABD∽△ACB;
(2)若AD=5,AB= 7,求AC的长.
如,已知抛物线y = ax2+bx+ c经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),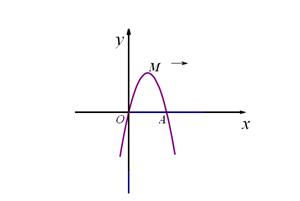
(1)求该抛物线的解析式;
(2)现将它向右平移m(m>0)个单位,所得抛物线与x轴交于C、D两点,与原抛物线交于点P,△CDP的面积为S,求S关于m的关系式;
(3)如图,以点A为圆心,以线段OA为半径画圆交抛物线y = ax2+bx+ c的对称轴于点B,连结AB,
若将抛物线向右平移m(m>0)个单位后,B点的对应点为B′,A点的对应点为A′点,且满足四边形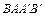 为菱形,平移后的抛物线的对称轴与菱形的对角线BA′交于点E,在x轴上是否存在一点F,
为菱形,平移后的抛物线的对称轴与菱形的对角线BA′交于点E,在x轴上是否存在一点F,
使得以E、F、A′为顶点的三角形与△BAE相似,若存在求出F点坐标,若不存在说明理由. 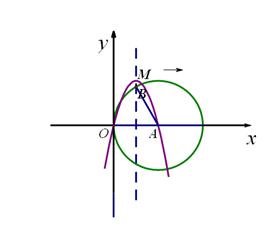
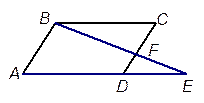
如图,在平行四边形ABCD中,E为边AD延长线上的一点,且D为AE的黄金分割点,即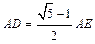 ,BE交DC于点F,已知
,BE交DC于点F,已知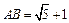 ,求CF的长 .
,求CF的长 .