已知数列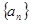 满足:
满足: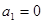 ,
,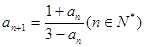
(Ⅰ)计算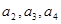 的值;
的值;
(Ⅱ)由(Ⅰ)的结果猜想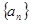 的通项公式,并用数学归纳法证明你的结论.
的通项公式,并用数学归纳法证明你的结论.
设函数 ,其中向量
,其中向量
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)在ΔABC中,角A、B、C所对的边分别为a、b、c,若 ,且
,且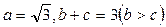 ,求
,求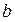 与
与 的值。
的值。
已知等差数列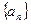 中,
中, ,前10项和
,前10项和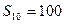 .
.
(1)求数列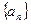 的通项公式;
的通项公式;
(2)设 ,证明
,证明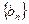 为等比数列,并求
为等比数列,并求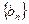 的前四项之和。
的前四项之和。
(3)设 ,求
,求 的前五项之和。
的前五项之和。
(1)已知 ,
, ,求
,求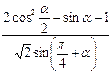 的值;
的值;
(2)已知 ,且
,且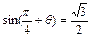 ,求
,求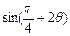 的值
的值
设M是由满足下列条件的函数 构成的集合:“①方
构成的集合:“①方 有实数根;②函数
有实数根;②函数 的导数
的导数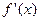 满足
满足 ”
”
(I)证明:函数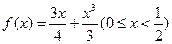 是集合M中的元素;
是集合M中的元素;
(II)证明:函数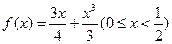 具有下面的性质:对于任意
具有下面的性质:对于任意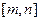
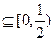 ,都存在
,都存在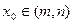 ,使得等式
,使得等式 成立。
成立。
(15 分)已知椭圆的右焦点F 与抛物线y2 =" 4x" 的焦点重合,短轴长为2.椭圆的右准线l与x轴交于E,过右焦点F 的直线与椭圆相交于A、B 两点,点C 在右准线l上,BC//x 轴.
(1)求椭圆的标准方程,并指出其离心率;
(2)求证:线段EF被直线AC 平分.