某同学参加北大、清华、科大三所学校的自主命题招生考试,其被录取的概率分别为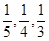 (各学校是否录取他相互独立,允许他可以被多个学校同时录取).
(各学校是否录取他相互独立,允许他可以被多个学校同时录取).
(Ⅰ)求此同学没有被任何学校录取的概率;
(Ⅱ)求此同学至少被两所学校录取的概率.
过点P(3,6)的直线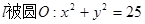 截得的弦AB的长为8,求直线
截得的弦AB的长为8,求直线
设直线 交于点
交于点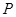 .
.
(1)求点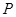 的坐标;
的坐标;
(2)当直线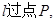 且与直线
且与直线 垂直时,求直线
垂直时,求直线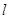 的方程.
的方程.
已知函数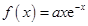
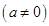 .
.
(1)求函数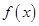 的单调区间;
的单调区间;
(2)当 时,
时,
(I)已知函数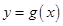 的图象与函数
的图象与函数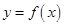 的图象关于直线
的图象关于直线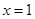 对称.证明当
对称.证明当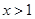 时,
时,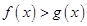 ;
;
(II)如果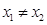 ,且
,且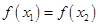 ,证明
,证明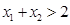 .
.
如图,已知椭圆C: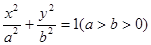 的左、右焦点为
的左、右焦点为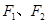 ,其上顶点为
,其上顶点为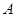 .已知
.已知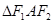 是边长为
是边长为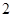 的正三角形.
的正三角形.
(1)求椭圆C的方程;
(2) 过点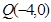 任作一直线
任作一直线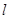 交椭圆C于
交椭圆C于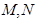 两点,记
两点,记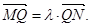 若在线段
若在线段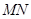 上取一点
上取一点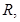 使得
使得 ,试判断当直线
,试判断当直线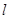 运动时,点
运动时,点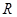 是否在某一定直线上运动?若在,请求出该定直线的方程,若不在,请说明理由.
是否在某一定直线上运动?若在,请求出该定直线的方程,若不在,请说明理由.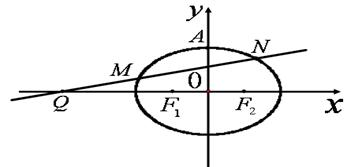
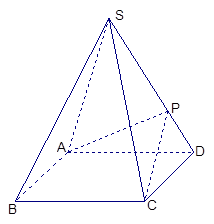
如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.
(1)求证:AC⊥SD;
(2)若SD⊥平面PAC,求二面角P-AC-D的大小
(3)在(2)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC.若存在,求SE:EC的值;若不存在,试说明理由.