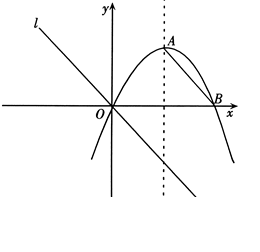
如图,对称轴为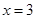 的抛物线
的抛物线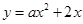 与
与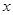 轴相交于点
轴相交于点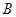 、
、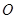
求抛物线的解析式,并求出顶点
 的坐标
的坐标连结AB,把AB所在的直线平移,使它经过原点O,得到直线
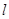 .点P是
.点P是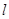 上一动点.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为
上一动点.设以点A、B、O、P为顶点的四边形面积为S,点P的横坐标为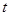 ,当0<S≤18时,求
,当0<S≤18时,求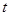 的取值范围
的取值范围在(2)的条件下,当
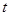 取最大值时,抛物线上是否存在点
取最大值时,抛物线上是否存在点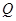 ,使△OP
,使△OP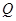 为直角三角形且OP为直角边.若存在,直接写出点
为直角三角形且OP为直角边.若存在,直接写出点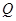 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
计算: .
.
如图,平面直角坐标系xOy中, Rt△AOB的直角边OA在x轴的正半轴上,点B在第一象限,并且AB=3,OA=6,将△AOB绕点O逆时针旋转90度得到△COD.点P从点C出发(不含点C),沿射线DC方向运动,记过点D,P,B的抛物线的解析式为y=ax2+bx+c(a<0). 
(1)直接写出点D的坐标;
(2)在直线CD的上方是否存在一点Q,使得点D,O,P,Q四点构成的四边形是菱形,若存在,求出P与Q的坐标;
(3)当点P运动到∠DOP=45度时,求抛物线的对称轴;
(4)求代数式a+b+c的值的取值范围(直接写出答案即可).
如图①是矩形包书纸的示意图,虚线是折痕,四个角均为大小相同的正方形,正方形的边长为折叠进去的宽度.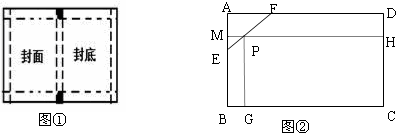
(1)现有一本书长为25cm,宽为20cm,厚度是2cm,如果按照如图①的包书方式,并且折叠进去的宽度是3cm,则需要书包纸的长和宽分别为多少?(请直接写出答案).
(2)已知数学课本长为26 cm,宽为18.5cm,厚为1cm,小明用一张面积为1260cm2的矩形书包纸按如图①包好了这本书,求折进去的宽度.
(3)如图②,矩形ABCD是一张一个角(△AEF)被污损的书包纸,已知AB=30,BC=50,AE=12,AF=16,要使用没有污损的部分包一本长为19,宽为16,厚为6的字典,小红认为只要按如图②的剪裁方式剪出一张面积最大的矩形PGCH就能包好这本字典. 设PM=x,矩形PGCH的面积为y,当x取何值时y最大?并由此判断小红的想法是否可行.
如图,在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30°.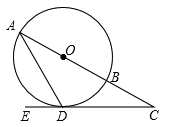
(1)判断直线CD是否为⊙O的切线,请说明理由;
(2)若CD="3" ,求BC的长.
已知一次函数y=kx+b的图象经过点A(-1,3)和点B(2,-3).
(1)求这个一次函数的解析式;
(2)当x取何值时,函数值 ?
?