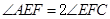如图,平面直角坐标系xOy中, Rt△AOB的直角边OA在x轴的正半轴上,点B在第一象限,并且AB=3,OA=6,将△AOB绕点O逆时针旋转90度得到△COD.点P从点C出发(不含点C),沿射线DC方向运动,记过点D,P,B的抛物线的解析式为y=ax2+bx+c(a<0). 
(1)直接写出点D的坐标;
(2)在直线CD的上方是否存在一点Q,使得点D,O,P,Q四点构成的四边形是菱形,若存在,求出P与Q的坐标;
(3)当点P运动到∠DOP=45度时,求抛物线的对称轴;
(4)求代数式a+b+c的值的取值范围(直接写出答案即可).
已知a、b、c是△ABC的三边,且满足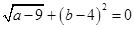 ,则第三边c的取值范围是.
,则第三边c的取值范围是.
写出一个实数k的值,使得正比例函数y= 的图象在二、四象限.
的图象在二、四象限.
函数y= 中自变量x的取值范围是.
中自变量x的取值范围是.
如图,抛物线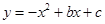 与x轴交于
与x轴交于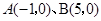 两点,直线
两点,直线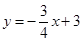 与y 轴交于点
与y 轴交于点 ,与
,与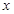 轴交于点
轴交于点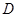 ,点
,点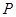 是
是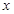 轴上方的抛物线上一动点,过点
轴上方的抛物线上一动点,过点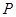 作
作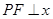 轴于点
轴于点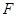 ,交直线
,交直线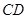 于点
于点 .设点
.设点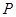 的横坐标为
的横坐标为 。
。
(1)求抛物线的解析式;
(2)若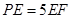 ,求
,求 的值;
的值;
(3)若点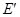 是点
是点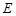 关于直线
关于直线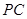 的对称点、是否存在点
的对称点、是否存在点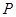 ,使点
,使点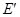 落在y轴上?若存在,求出相应的点
落在y轴上?若存在,求出相应的点 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
如图,□ABCD中,点E是BC边上的一点,且DE=BC,过点A作AF⊥CD于点F,交DE于点G,连结AE、EF.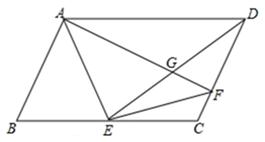
(1)若AE平分∠BAF,求证:BE=EG;
(2若点 是
是 边上的中点,求证:
边上的中点,求证: