如图,在Rt△ABC中,∠ACB=90°,AC=6㎝,BC=8㎝,P为BC的中点.动点Q从点P出发,沿射线PC方向以2㎝/s的速度运动,以P为圆心,PQ长为半径作圆.设点Q运动的时间为t s.
当t="1.2" s时,判断直线AB与⊙P的位置关系,并说明理由
已知⊙O为△ABC的外接圆,若⊙P与⊙O相切,求t的值
如图,∠B=∠C=90°,M是BC的中点,DM平分∠ADC,则AM平分∠DAB吗?试说明理由。(提示:过点M作ME垂直AD于E)。
如图:△ABC中,AB=AC=5,AB的垂直平分线DE交AB、AC于E、D,
(1)若△BCD的周长为8,求BC的长;
(2)若BC=4,求△BCD的周长.
如图,方格纸中的每个小方格都是边长为1的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,A(-1,5),B(-1,0),C(-4,3).
(1)画出△ABC关于y轴对称的△A1B1C1;(其中A1、B1、C1是A、B、C的对应点,不写画法)
(2)写出A1、B1、C1的坐标;
(3)求出△A1B1C1的面积.
在Rt△ABC中,∠BAC=90°,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.问△AEF与△DEB全等吗?说明理由。

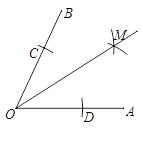
根据图中尺规作图的痕迹,先判断得出结论: .
然后证明你的结论(不要求写出已知、求证).