如图，是一个用六根竹条连接而成的凸六边形风筝骨架，考虑到骨架的稳固性、美观性、实用性等因素，需再加竹条与其顶点连接。要求：在图（1）、（2）中分别加适当根竹条，设计出两种不同的连接方案；
通过上面的设计，可以看出至少需再加几根竹条，才能保证风筝骨架稳固、美观和实用？直接回答： ；
在上面的方案设计过程中，你所应用的数学道理是 .
甲、乙、丙、丁4名同学进行一次羽毛球单打比赛，要从中选出2名同学打第一场比赛，求下列事件的概率．
（1）已确定甲打第一场，再从其余3名同学中随机抽取1名，恰好选中乙同学；
（2）随机选取2名同学，其中有乙同学．
求抛物线y=﹣2x2+8x﹣8的开口方向、对称轴及顶点坐标．
已知△ABC是正三角形，正方形EFPN的顶点E、F在边AB上，顶点N在边AC上．
（1）如图，在正三角形ABC及其内部，以点A为位似中心，画出正方形EFPN的位似正方形E′F′P′N′，且使正方形E′F′P′N′的面积最大（不谢画法，但要保留画图痕迹）；
（2）若正三角形ABC的边长为3+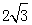 
，则（1）中画出的正方形E′F′P′N′的边长为．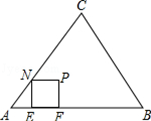
如图，一条直线与反比例函数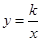
的图象交于A（1，4）
B（4，n）两点，与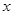
轴交于D点，AC⊥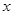轴，垂足为C．
（1）如图甲，①求反比例函数的解析式；②求n的值及D点坐标；
（2）如图乙，若点E在线段AD上运动，连结CE，作∠CEF=45°，EF交AC于F点．
①试说明△CDE∽△EAF；
②当△ECF为等腰三角形时，直接写出F点坐标．
如图，是小亮晚上在广场散步的示意图，图中线段AB表示站立在广场上的小亮，线段PO表示直立在广场上的灯杆，点P表示照明灯的位置．
（1）在小亮由B处沿BO所在的方向行走到达O处的过程中，他在地面上的影子长度的变化情况为；
（2）请你在图中画出小亮站在AB处的影子；
（3）当小亮离开灯杆的距离OB=4.2m时，身高（AB）为1.6m的小亮的影长为1.6m，问当小亮离开灯杆的距离OD=6m时，小亮的影长是多少m？