(本小题13分) 已知函数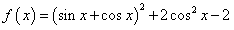 .(Ⅰ)求
.(Ⅰ)求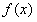 函数图象的对称轴方程;(Ⅱ)求
函数图象的对称轴方程;(Ⅱ)求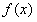 的单调增区间;(Ⅲ)当
的单调增区间;(Ⅲ)当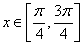 时,求函数
时,求函数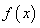 的最大值,最小值.
的最大值,最小值.
(本小题满分13分)在 中,
中, ,
,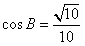 .(Ⅰ)求角
.(Ⅰ)求角 ;(Ⅱ)设
;(Ⅱ)设 ,求
,求 的面积.
的面积.
(本小题满分14分)
已知函数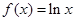 ,
, ,函数
,函数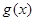 的图象在点
的图象在点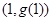 处的切线平行于
处的切线平行于 轴.
轴.
(1)确定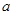 与
与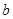 的关系;
的关系;
(2)试讨论函数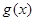 的单调性;
的单调性;
(3)证明:对任意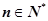 ,都有
,都有 成立.
成立.
(本小题满分14分)
已知函数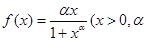 为常数,数列
为常数,数列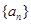 满足:
满足: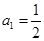 ,
,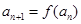 ,
, .
.
(1)当 时,求数列
时,求数列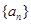 的通项公式;
的通项公式;
(2)在(1)的条件下,证明对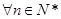 有:
有: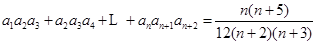 ;
;
(3)若 ,且对
,且对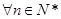 ,有
,有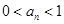 ,证明:
,证明: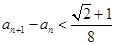 .
.
(本小题满分14分)
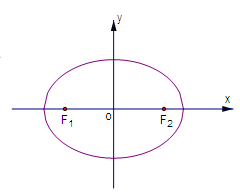
如图,设点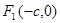 、
、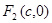 分别是椭圆
分别是椭圆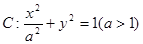 的左、右焦点,
的左、右焦点,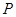 为椭圆
为椭圆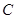 上任意一点,且
上任意一点,且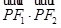 最小值为
最小值为 .
.
(1)求椭圆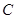 的方程;
的方程;
(2)若动直线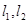 均与椭圆
均与椭圆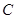 相切,且
相切,且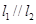 ,试探究在
,试探究在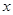 轴上是否存在定点
轴上是否存在定点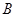 ,点
,点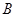 到
到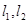 的距离之积恒为1?若存在,请求出点
的距离之积恒为1?若存在,请求出点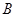 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.