(本小题满分14分)
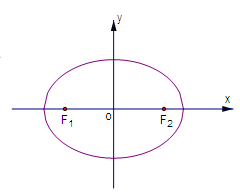
如图,设点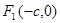 、
、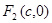 分别是椭圆
分别是椭圆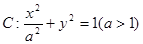 的左、右焦点,
的左、右焦点,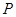 为椭圆
为椭圆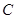 上任意一点,且
上任意一点,且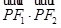 最小值为
最小值为 .
.
(1)求椭圆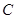 的方程;
的方程;
(2)若动直线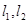 均与椭圆
均与椭圆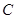 相切,且
相切,且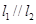 ,试探究在
,试探究在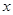 轴上是否存在定点
轴上是否存在定点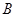 ,点
,点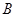 到
到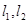 的距离之积恒为1?若存在,请求出点
的距离之积恒为1?若存在,请求出点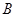 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
甲、乙两人约好在“五、一”长假时间去天水市石马坪南山牡丹园观花游玩,决定在早晨7点半到8点半之间在石马坪的惠民商场门口会面,并约定先到者等候另一人15分钟,若未等到,即可离开惠民商场门口,直接去牡丹园观花,大家算一算在“五、一”这一天两人会面后一起去观花的概率是多少?
将一颗骰子先后抛掷2次,观察向上的点数,则以第一次向上点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在圆x2+y2=27的内部的概率.
某工厂对某产品的产量与单位成本的资料分析后有如下数据:
| 月份 |
1 |
2 |
3 |
4 |
5 |
6 |
| 产量x千件 |
2 |
3 |
4 |
3 |
4 |
5 |
| 单位成本y元/件 |
73 |
72 |
71 |
73 |
69 |
68 |
(Ⅰ) 画出散点图,并判断产量与单位成本是否线性相关。
(Ⅱ) 求单位成本y与月产量x之间的线性回归方程。(其中已计算得: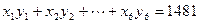 ,结果保留两位小数)
,结果保留两位小数)
已知曲线C1: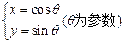 ,曲线C2:
,曲线C2: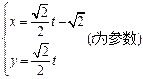 .
.
(1)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(2)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线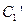 ,
,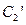 .写出
.写出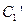 ,
,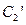 的参数方程.
的参数方程.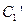 与
与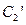 公共点的个数和C1与C2公共点的个数是否相同?说明你的理由.
公共点的个数和C1与C2公共点的个数是否相同?说明你的理由.
已知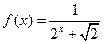 ,分别求
,分别求 ,
,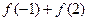 ,
,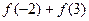 ,然后归纳猜想一般性结论,并证明你的结论.
,然后归纳猜想一般性结论,并证明你的结论.