甲、乙两人约好在“五、一”长假时间去天水市石马坪南山牡丹园观花游玩,决定在早晨7点半到8点半之间在石马坪的惠民商场门口会面,并约定先到者等候另一人15分钟,若未等到,即可离开惠民商场门口,直接去牡丹园观花,大家算一算在“五、一”这一天两人会面后一起去观花的概率是多少?
(本小题满分12分)
已知 三个内角
三个内角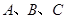 的对边分别为
的对边分别为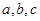 ,
,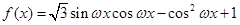
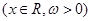 的图象与直线
的图象与直线 相切,且切点横坐标依次成公差为
相切,且切点横坐标依次成公差为 的等差数列,点
的等差数列,点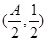 是函数
是函数 的一个对称中心.
的一个对称中心.
(Ⅰ)求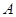 的大小;
的大小;
(Ⅱ)已知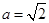 ,
,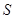 为
为 的面积,求
的面积,求 的最大值及此时B的值.
的最大值及此时B的值.
(本小题满分13分)
已知数列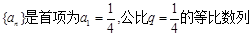 ,设
,设  ,数列
,数列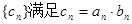 .
.
(I)求证: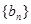 是等差数列;
是等差数列;
(II)求数列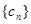 的前n项和Sn;
的前n项和Sn;
(Ⅲ)若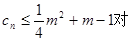 一切正整数n恒成立,求实数m的取值范围.
一切正整数n恒成立,求实数m的取值范围.
(本小题满分13分)
抛物线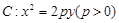 上一点
上一点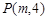 到其焦点的距离为5.
到其焦点的距离为5.
(I)求 与
与 的值;
的值;
(II)若直线 与抛物线
与抛物线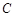 相交于
相交于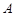 、
、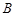 两点,
两点,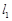 、
、 分别是该抛物线在
分别是该抛物线在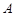 、
、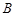 两点处的切线,
两点处的切线, 、
、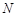 分别是
分别是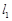 、
、 与该抛物线的准线交点,求证:
与该抛物线的准线交点,求证: .
.
(本小题满分13分)已知函数 ,其中
,其中 为自然对数的底数.
为自然对数的底数.
(Ⅰ)当 时,求曲线
时,求曲线 在
在 处的切线与坐标轴围成的面积;
处的切线与坐标轴围成的面积;
(Ⅱ)若函数 存在一个极大值点和一个极小值点,且极大值与极小值的积为
存在一个极大值点和一个极小值点,且极大值与极小值的积为 ,求
,求 的值.
的值.
(本小题满分12分)科研所研究人员都具有本科和研究生两类学历,年龄段和学历如下表,从该科研所任选一名研究人员,是本科生概率是 ,是35岁以下的研究生概率是
,是35岁以下的研究生概率是 .
.
(Ⅰ)求出表格中的 和
和 的值;
的值;
(Ⅱ)设“从数学教研组任选两名教师,本科一名,研究生一名,50岁以上本科生和35岁以下的研究生不全选中” 的事件为A,求事件A概率P(A).