(本小题满分12分)
已知 三个内角
三个内角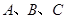 的对边分别为
的对边分别为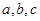 ,
,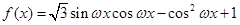
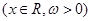 的图象与直线
的图象与直线 相切,且切点横坐标依次成公差为
相切,且切点横坐标依次成公差为 的等差数列,点
的等差数列,点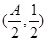 是函数
是函数 的一个对称中心.
的一个对称中心.
(Ⅰ)求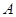 的大小;
的大小;
(Ⅱ)已知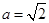 ,
,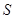 为
为 的面积,求
的面积,求 的最大值及此时B的值.
的最大值及此时B的值.
(本题满分12分)
如图,甲船以每小时30 海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10
海里的速度向正北方向航行,乙船按固定方向匀速直线航行.当甲船位于A1处时,乙船位于甲船的北偏西105°方向的B1处,此时两船相距20海里.当甲船航行20分钟到达A2处时,乙船航行到甲船的北偏西120°方向的B2处,此时两船相距10 海里,问乙船每小时航行多少海里?
海里,问乙船每小时航行多少海里?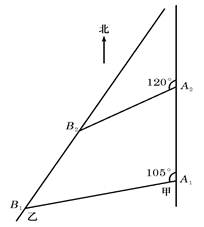
已知数列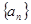 的通项公式为
的通项公式为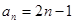 ,数列
,数列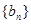 的前n项和为
的前n项和为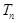 ,且满足
,且满足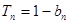
(1)求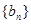 的通项公式;
的通项公式;
(2)在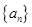 中是否存在使得
中是否存在使得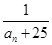 是
是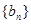 中的项,若存在,请写出满足题意的一项(不要求写出所有的项);若不存在,请说明理由.
中的项,若存在,请写出满足题意的一项(不要求写出所有的项);若不存在,请说明理由.
已知函数f(x)=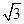 cos2x+sinxcosx
cos2x+sinxcosx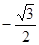 .
.
(1)求函数f(x)的单调递增区间;
(2)若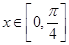 ,求函数f(x)的取值范围;
,求函数f(x)的取值范围;
(本小题满分14分)设数列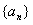 的首项
的首项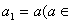 R),且
R),且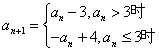 ,
,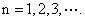 (Ⅰ)若
(Ⅰ)若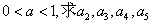 ;(Ⅱ)若
;(Ⅱ)若 ,证明:
,证明: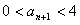 ;(Ⅲ)若
;(Ⅲ)若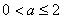 ,求所有的正整数
,求所有的正整数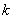 ,使得对于任意
,使得对于任意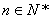 ,均有
,均有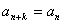 成立.
成立.
(本小题满分14分)
已知函数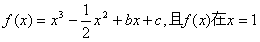 处取得极值.
处取得极值.
(Ⅰ)求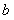 的值;
的值;
(Ⅱ)若当 恒成立,求
恒成立,求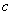 的取值范围;
的取值范围;
(Ⅲ)对任意的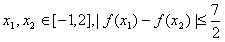 是否恒成立?如果成立,给出证明,如果不成立,请说明理由.
是否恒成立?如果成立,给出证明,如果不成立,请说明理由.