计算(本题满分12分,每题4分)
(1) ―12012 + (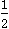 )-1―(3.14-π)0
)-1―(3.14-π)0
(2) (-6xy2)2(― xy +
xy + 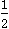 y2 ―x2)
y2 ―x2)
(3) 先化简,再求值:(2m+n)2-(3m-n)2+5m(m-n),其中m=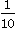 ,n=
,n=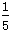 .
.
2009年某市出口贸易总值为22.52亿美元,至2011年出口贸易总值达到50.67亿美元,反映了两年来该市出口贸易的高速增长.
(1)求这两年该市出口贸易的年平均增长率;
(2)按这样的速度增长,请你预测2012年该市的出口贸易总值.
(提示:2252=4×563,5067=9×563)
如图,在平行四边形ABCD中,点P是对角线AC上的一点,PE⊥AB,PF⊥AD,垂足分别为E、F,且PE=PF,平行四边形ABCD是菱形吗?为什么?
某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).请你根据图中所给的信息解答下列问题:
(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有多少人达标?
(3)若该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?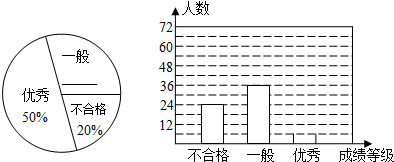
如图,AB是⊙O的直径, =
=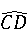 ,∠COD=60°
,∠COD=60°
(1)△AOC是等边三角形吗?请说明理由;(2)求证:OC∥BD.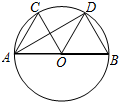
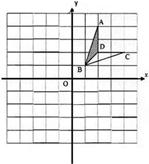
如图,下列网格中,每个小方格的边长都是1.(1)分别作出四边形ABCD关于x轴、y轴、原点的对称图形;(2)求出四边形ABCD的面积.