某汽车制造厂开发一款新式电动汽车,计划一年生产安装240辆。由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人.他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘n(0<n<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
(3)在(2)的条件下,工厂给安装电动汽车的每名熟练工每月发2000元的工资,给每名新工人每月发1200元的工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时工厂每月支出的工资总额W(元)尽可能的少?
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B。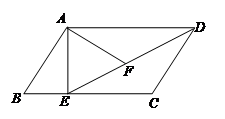
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6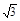 ,AF=4
,AF=4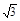 ,求AE的长。
,求AE的长。
公园中有一棵树和一座塔恰好座落在一条笔直的道路上.在途中A处,小杰测得树顶和塔尖的仰角分别为45º和30º,继续前进8米至B处,又测得树顶和塔尖的仰角分别为16º和45º,试问这棵树和这座塔的高度分别为多少米?(结果精确0.1米.参考数据: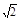 ≈1.414,
≈1.414,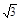 ≈1.732,tan16º≈0.287,sin16º≈0.276,cos16º≈0.961)
≈1.732,tan16º≈0.287,sin16º≈0.276,cos16º≈0.961)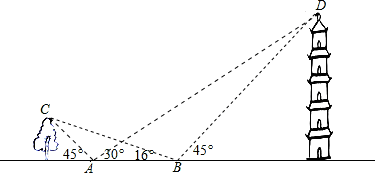
近年某高中招生制度改革,实行自主招生。某初中学校获得保送(指标生)名额若干,现在九年级四位品学兼优的学生小斌(男)、小亮(男)、小红(女)、小丽(女)都获得保送资格,且机会均等。
(1)、若学校只有一个名额,则随机选到小斌的概率是
(2)、若学校争取到两个名额,请用树状图或列表法求随机选到保送的学生恰好是一男一女的概率。
先化简,后求值: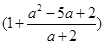
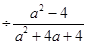 ,其中
,其中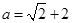
如图,在△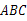 中,∠
中,∠ 90°,
90°, ,
, ,点
,点 从点
从点 出发,沿
出发,沿 以
以
2㎝ 的速度向点
的速度向点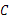 移动,点
移动,点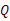 从点
从点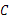 出发,以
出发,以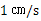 的速度向点
的速度向点 移动,若点
移动,若点 分别从点
分别从点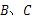 同时出发,
同时出发,
设运动时间为 ,当
,当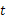 为何值时,△
为何值时,△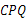 与△
与△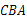 相似?
相似?