问题提出
我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0,则M<N.
问题解决
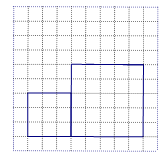
如图1,把边长为a+b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个矩形,试比较两个小正方形面积之和M与两个矩形面积之和N的大小.
解:由图可知:M=a2+b2,N=2ab.
∴M-N=a2+b2-2ab=(a-b)2.
∵a≠b,∴(a-b)2>0.
∴M-N>0.
∴M>N.
类比应用已知:多项式M =2a2-a+1 ,N =a2-2a.试比较M与N的大小.
已知:如图,锐角△ABC (其中BC为a,AC为b,AB为c)三边
满足a <b < c ,现将△ABC 补成长方形,使得△ABC的两个顶
点为长方形的两个端点,第三个顶点落在长方形的这一边的对边上。
①这样的长方形可以画 个;
②所画的长方形中哪个周长最小?为什么?
拓展延伸
已知:如图,锐角△ABC (其中BC为a,AC为b,AB为c)三边满足a <b < c ,画其BC边上的内接正方形EFGH , 使E、F两点在边BC上,G、H分别在边AC、AB上,同样还可画AC、AB边上的内接正方形,问哪条边上的内接正方形面积最大?为什么?
已知如图1,Rt△ABC和Rt△ADE的直角边AC和AE重叠在一起,AD=AE,∠B=30°,∠DAE=∠ACB=90°.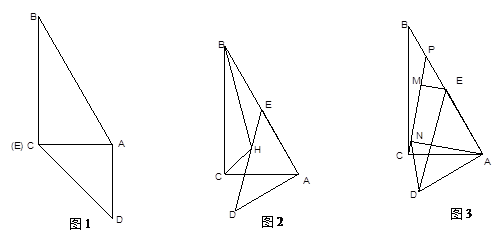
(1)如图1,填空:∠BAD= ;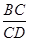 = ;
= ;
(2)如图2,将△ADE绕点A顺时针旋转,使AE到AB边上,∠ACH=∠BCH,连接BH,求∠CBH的度数;
(3)如图3,点P是BE上一点,过A、E两点分别作AN⊥PC、EM⊥PC,垂足分别为N、M,若EM=2,AN=5,求△AND的面积.
如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E. ⊙O的切线BF与弦AD的延长线相交于点F,且AD=3,cos∠BCD=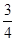 .
.
(1)求证:CD∥BF;
(2)求⊙O的半径;
(3)求弦CD的长. 
如图,一辆汽车在一个十字路口遇到红灯刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°,如果斑马线的宽度AB=3米,驾驶员与车头的距离是0.8米,这时汽车车头与斑马线的距离x是多少? 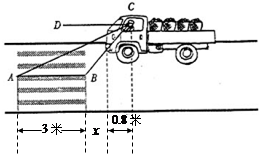
图1是某城市四月份1至8日的日最高气温随时间变化的折线统计图,小刚根据图1将数据统计整理后制成了图2.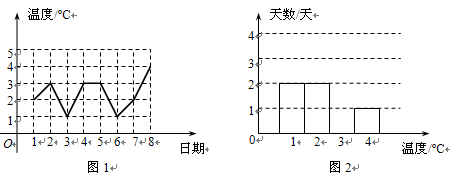
根据图中信息,解答下列问题:
(1)将图2补充完整;
(2)这8天的日最高气温的中位数是 ºC;
(3)计算这8天的日最高气温的平均数.
已知两个连体的正方形(有两条边在同一条直线上)在正方形网格上的位置如图所示,请你把它分割后,拼接成一个新的正方形. (要求:在正方形网格图中用实线画出拼接成的新正方形且新正方形的顶点在网格的格点上,不写作法).