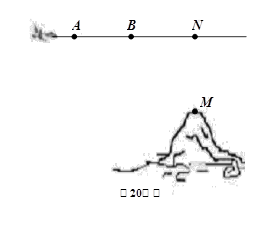
如图,飞机沿水平方向(A、B两点所在直线)飞行,前方有一座高山,为了避免飞机飞行过低,就必须测量山顶M到飞行路线AB的距离MN.飞机能够测量的数据有俯角和飞行距离(因安全因素,飞机不能飞到山顶M的正上方N处才测飞行距离),请你设计一个求距离MN的方案,要求指出需要测量的数据(用字母表示,并在图中标出)
用你所设计测出的数据写出求距离MN的步骤
先化简 ,然后从
,然后从 ,1,-1中选取一个你认为合适的数作为x的值代入求值.
,1,-1中选取一个你认为合适的数作为x的值代入求值.
(1)计算: (2)解不等式组
(2)解不等式组
2011年3月10日12时58分,在云南盈江县发生5.8级地震,随后又相继发生里氏4.7级、里氏4.5级、里氏3.6级余震。灾情发生后,全国人民抗震救灾,众志成城。湖州市政府也筹集了抗震救灾物资共120吨准备运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
| 车型 |
甲 |
乙 |
丙 |
| 汽车运载量(吨/辆) |
5 |
8 |
10 |
| 汽车运费(元/辆) |
400 |
500 |
600 |
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,市政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总车辆数为14辆,你能分别求出三种车型的车辆数吗?此时的运费又是多少元?
如图a,△ABC和△CEF是两个大小不等的等边三角形(等边三角形为三条边相等,三个角为60°的三角形),且有一个公共顶点C,点F、B、C在同一直线上,连结AF和BE。
(1)线段AF和BE有怎样的大小关系?(写出结论,不需要说明理由)
(2)将图a中的△CEF绕点C旋转一定的角度,得到图b,(1)中的结论还成立吗?作出判断并说明理由;
在学习“轴对称现象”内容时,老师让同学们寻找身边的轴对称图形,小明有一副三角尺和一个量角器(如图所示).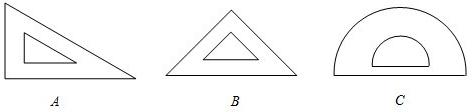
(1)小明的这三件文具中,可以看做是轴对称图形的是____________(填字母代号);
(2)小红也有同样的一副三角尺和一个量角器,若他们分别从自己这三件文具中随机取出一件,则可以拼成一个轴对称图案的概率是多少?(请画树状图或列表)计算)