有一种沙漠蝎子既没有眼睛,也没有耳朵,它捕食猎物靠的是一种地震仪式的本领,它有八条腿,趴伏时大致对称地放置在躯体四周(如图12所示),不远处的小虫一有骚动,就会在沙面上引起一阵地震波,蝎子从哪只腿先感到地震波就能判断小虫所在的方向,并从P波和S波到达的时间差就可以“算出”小虫到它的距离。方位和距离都知道了,它就能扑上去捕获小虫了,已知P波速度为150m/s,S波速度为50m/s,如果两波到达沙漠蝎子的时间差为 s,则小虫离它的距离多大?
s,则小虫离它的距离多大?
(8分)如图所示电路中,电源电动势E=12V,内阻r=1 ,电阻R1=9
,电阻R1=9 ,R2=5
,R2=5 ,R3是一只滑动变阻器,其阻值变化范围为0~20
,R3是一只滑动变阻器,其阻值变化范围为0~20 。求:
。求:
(1)电流表的示数为0.4A时,R3的阻值为多大?
(2)当R3为多大时电源的总功率最大?最大功率是多少?
做匀变速运动的物体,在第一个4秒内的位移为24米,第二个4秒内的位移为60米,
求(1).物体的加速度是多少?(2)、物体的初速度是多少?
飞机着陆后以6m/s2的加速度匀减速运动,若着陆时的速度为120m/s.
试求:(1)飞机着陆后15s末时的速度
(2)飞机着陆后25s内的位移
从离地面80m高的空中自由落下一个小球,g取10m/s2,求:
(1)小球第2s末的速度是多少?
(2) 小球最后1s内通过的高度是多少?
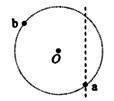
如图,一半径为R的圆表示一柱形区域的横截面(纸面)。在柱形区域内加一方向垂直于纸面的匀强磁场,一质量为m、电荷量为q的粒子沿图中直线在圆上的a点射入柱形区域,在圆上的b点离开该区域,离开时速度方向与直线垂直。圆心O到直线的距离为  。现将磁场换为平行于纸面且垂直于直线的匀强电场,同一粒子以同样
。现将磁场换为平行于纸面且垂直于直线的匀强电场,同一粒子以同样
速度沿直线在a点射入柱形区域,也在b点离开该区域。若磁感应强度大小为B,不计重力,求:(1)求粒子在匀强磁场中做圆周运动的半径。(2) 电场强度的大小。