在“验证机械能守恒定律”的一次实验中,质量m=1kg的重物自由下落,在纸带上打出一系列的点,如图所示(相邻记数点时间间隔为0.02s),
那么:
(1)纸带的________(用字母表示)端与重物相连;
(2)打点计时器打下计数点B时,物体的速度vB=________;
(3)从起点P到打下计数点B的过程中物体的重力势能减少量△EP=________,此过程中物体动能的增加量△Ek=________;(g取9.8m/s2)
(4)通过计算,数值上△EP________△Ek(填“<”、“>”或“=”),这是因为____________;
(5)实验的结论是____________________________________________________.
下述关于用多用表欧姆档测电阻的说法中错洖的是
| A.测量电阻时,如果红、黑表笔分别插在负、正插孔,不会影响测量结果 |
| B.测量电路中的某个电阻,应该把该电阻与电路断开 |
| C.测量阻值不同的电阻时都必须重新电阻调零 |
| D.测量阻值不同的电阻时,只要不换档就不需重新电阻调零 |
某同学在做“探究小车速度随时间变化的规律”实验时,得到了如下图所示的一条较为理想的纸带,A、B、C、D、E、F为在纸带上依次所选的记数点,相邻记数点间有四个点未画出,测得AB=1.20cm,AC="3." 20cm,AD=6.00cm,AE=9.60cm,AF=14.00cm,则以上由数据可知小车做运动,小车运动的加速度a=m/s2,打点计时器打下D点时小车的瞬时速度为m/s。(计算结果小数点后保留两位)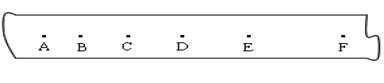
电磁打点计时器通常的工作电压为,电火花打点计时器通常的工作电压为。我们日常生活所用的交流电频率是50Hz,如果用它做电源,打点计时器每隔s打一个点。
某同学在做“探究小车速度随时间变化规律”的实验时,得到一条点迹清晰的纸带如图,在纸带上依次选出7个计数点,分别标以O、A、B、C、D、E和F,每相邻的两个计数点间还有四个点未画出,打点计时器所用电源的频率是50Hz。
①如果测得C、D两点间距S4=2.70cm,D、E两点间距S5=2.90cm,则据此数据计算在打D点时小车的速度公式为,小车的速度值vD=m/s。(保留三位有效数字)
②该同学分别算出其它速度:vA=0.220m/s,vB=0.241m/s,vc=0.258m/s, vE="0.300m/s" ,请设计实验数据记录表格填入框中,并在坐标系中作出小车运动的v-t图像,设O点为计时起点。
③由所做v-t图像判断,小车所做的运动为。

某同学用如图所示的装置测定重力加速度,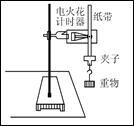
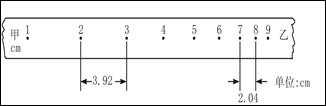
(1)电火花计时器的工作电压为____,频率为______。
(2)打出的纸带如图所示,实验时纸带的___端应和重物相连接。(选填“甲”或“乙”)
(3)由纸带所示数据可算出实验时的加速度为 m/s2。
(4)当地的重力加速度数值为9.80 m/s2,请列出测量值与当地重力加速度的值有差异的一个原因:。