如图，Rt△ABC中∠C=90°、∠A=30°，在AC边上取点O画圆使⊙O经过A、B两点，
求证：以O为圆心，以OC为半径的圆与AB相切.
下列结论正确的序号是 ．（少选酌情给分，多选、错均不给分）
①AO="2CO" ；
②AO="BC" ；
③延长BC交⊙O与D，则A、B、D是⊙O的三等分点．
④图中阴影面积为：
（本小题满分9分）今年入春以来，湖南省大部分地区发生了罕见的旱灾，连续几个月无有效降水.为抗旱救灾，驻湘某部计划为驻地村民新建水渠3600米，为使水渠能尽快投入使用，实际工作效率是原计划工作效率的1.8倍，结果提前20天完成修水渠任务.问原计划每天修水渠多少米？
（本小题满分7分）解不等式组
，并
把它的解集在数轴上表示出
来.
如图，在平面直角坐标系中，抛物线y＝x2＋mx＋n经过点A(3，0)、
B(0，
－3)，点P是直线AB上的动点，过点P作x轴的垂线
交抛物线于点M，设点P的横
坐标为t．
(1)分别求出直线AB和这条抛物线的解析式．
(2)若点P在第四象
限，连接AM、BM，当线段PM最长时，求△ABM的面积．
(3)是否存在这样的点P，使得以点P、M、B、O为顶点的四边形为平行四边形？若存在，请直接写出点P的横坐标；若不存在，请说明理由．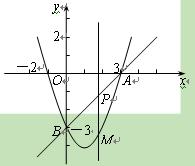
如图，已知CD是⊙O的直径，AC⊥CD，垂足为C，弦DE∥OA，直线AE、CD
相交于点B．
(1)求证：直线AB是⊙O的切线．
(2)当AC＝1，BE＝2，求tan∠OAC的值．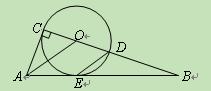
南宁市五象新区有长24000m的新建道路要铺上沥青．
(1)写出铺路所需时间t(天)与铺路速度v(m/天)的函数关系式．
(2)负责铺路的工程公司现有的铺路机每天最多能铺路400m，预计最快多少天可以完成铺路任务？
(3)为加快工程进度，公司决定投入不超过400万元的资金，购进10台更先进的铺路机．现有甲、乙两种机器可供选择，其中每种机器的价格和日铺路能力如下表．在原有的铺路机连续铺路40天后，新购进的10台机器加入铺路，公司要求至少比原来预计的时间提前10天完成任务．问有哪几种方案？请你通过计算说明选择哪种方案所用资金最少．