一列动车从甲地驶往乙地，一列快车从乙地驶往甲地，两车同时出发，行驶的时间为 x（h)，两车之间的距离为y (km) ，图中的折线表示y与x之间的函数关系．根据图象进行以下探究：甲、乙两地之间的距离为 km；
请解释图中点 B的实际意义；
求动车和快车的速度；
求线段BC 所表示的 x与y 之间的函数关系式，并写出自变量 x的取值范围；
若第二列动车也从甲地出发驶往乙地，速度与第一列动车相同．在第一列动车与快车相遇20分钟后，第二列动车与快车相遇．求第二列动车比第一列动车晚出发多少小时？
（本题8分）已知一个三位数的百位数字比十位数字大1，个位数字比十位数字小1，设十位数字为n。（1）用关于n的式子表示这个三位数（2）这个三位数一定能被3整除吗？说明理由。
(本题6分）化简求值：
（1）
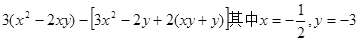
解方程（每小题4分，共8分）①
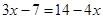
②3y－7＋4y＝6y－2.5
如图，在等边△ABC中，AD⊥BC于点D，一个直径与AD相等的圆与BC相切于点E，与AB相切于点F，连接EF。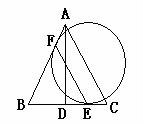
判断EF与AC的位置关系（不必说明理由）；
如图，过E作BC的垂线，交圆于G，连接AC，判断四边形ADEG的形状，并说明理由。
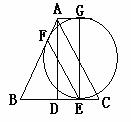
确定圆心O的位置，并说明理由。
探究下表中的奥妙，填空并完成下列题目
| 一元二次方程 |
两个根 |
二次三项式因式分解 |
 |
 |
 |
 |
 |
  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
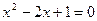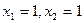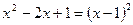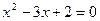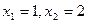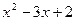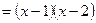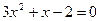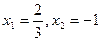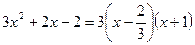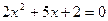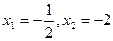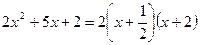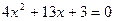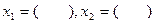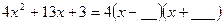如果一元二次方程
(
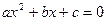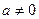)有解为
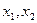，请你把二次三项式
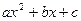因式分解。利用上面的结论，把二次三项式
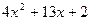因式分解。