设 .
.
(1)若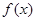 在
在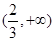 上存在单调递增区间,求
上存在单调递增区间,求 的取值范围;
的取值范围;
(2)当 时,
时,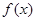 在
在 上的最小值为
上的最小值为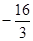 ,求
,求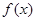 在该区间上的最大值.
在该区间上的最大值.
(本小题满分12分)下表是随机抽取的某市五个地段五种不同户型新电梯房面积 (单位:十平方米)和相应的房价
(单位:十平方米)和相应的房价 (单位:万元)统计表:
(单位:万元)统计表:
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
(Ⅰ)在给定的坐标系中画出散点图;
(Ⅱ)求用最小二乘法得到的回归直线方程(参考公式和数据: ,
, ,
, );
);
(Ⅲ)请估计该市一面积为
 的新电梯房的房价.
的新电梯房的房价.
(本题12分)已知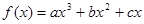 在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间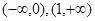 上是减函数,又
上是减函数,又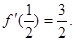
(Ⅰ)求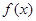 的解析式;
的解析式;
(Ⅱ)若在区间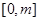 (m>0)上恒有
(m>0)上恒有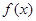 ≤x成立,求m的取值范围.
≤x成立,求m的取值范围.
(本小题满分12分)已知方程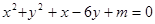
(1)若此方程表示的曲线是圆C,求m的取值范围;
(2)若(1)中的圆C与直线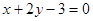 相交于P,Q两点,且
相交于P,Q两点,且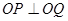 (O为原点),求圆C的方程.
(O为原点),求圆C的方程.
(本小题满分12分)
学校组织高考组考工作,为了搞好接待组委会招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余不喜爱。
(1)根据以上数据完成以下2×2列联表:
| 喜爱运动 |
不喜爱运动 |
总计 |
|
| 男 |
10 |
16 |
|
| 女 |
6 |
14 |
|
| 总计 |
30 |
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关?
(3)如果从喜欢运动的女志原者中(其中恰有4人会外语),抽取2名负责翻译工作,则抽出的志愿者中2人都能胜任翻译工作的概率是多少?
参考公式: ,其中
,其中
参考数据:
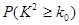 |
0.40 |
0.25 |
0.10 |
0.010 |
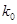 |
0.708 |
1.323 |
2.706 |
6.635 |
若正项数列 的前
的前 项和为
项和为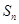 ,首项
,首项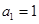 ,
,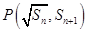 ,(
,(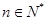 )在曲线
)在曲线 上.
上.
(1)求数列 的通项公式
的通项公式 ;
;
(2)设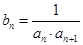 ,
,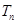 表示数列
表示数列 的前
的前 项和,求证:
项和,求证: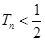 .
.