(本小题满分12分)
学校组织高考组考工作,为了搞好接待组委会招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余不喜爱。
(1)根据以上数据完成以下2×2列联表:
| |
喜爱运动 |
不喜爱运动 |
总计 |
| 男 |
10 |
|
16 |
| 女 |
6 |
|
14 |
| 总计 |
|
|
30 |
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关?
(3)如果从喜欢运动的女志原者中(其中恰有4人会外语),抽取2名负责翻译工作,则抽出的志愿者中2人都能胜任翻译工作的概率是多少?
参考公式: ,其中
,其中
参考数据:
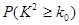 |
0.40 |
0.25 |
0.10 |
0.010 |
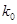 |
0.708 |
1.323 |
2.706 |
6.635 |
已知函数 ,
,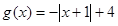 .
.
(1)若函数 的值不大于
的值不大于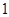 ,求
,求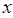 的取值范围;
的取值范围;
(2)若不等式 的解集为
的解集为 ,求
,求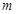 的取值范围.
的取值范围.
在直角坐标系 内,直线
内,直线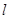 的参数方程
的参数方程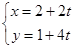 (
(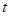 为参数),以
为参数),以 为极轴建立极坐标系,圆
为极轴建立极坐标系,圆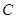 的极坐标方程为
的极坐标方程为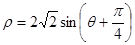 .
.
(1)求直线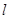 的普通方程和圆
的普通方程和圆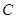 的直角坐标方程;
的直角坐标方程;
(2)确定直线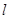 和圆
和圆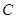 的位置关系.
的位置关系.
在直角坐标系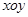 中,点
中,点 在矩阵
在矩阵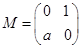 对应变换作用下得到点
对应变换作用下得到点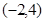 ,曲线
,曲线 在矩阵
在矩阵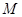 对应变换作用下得到曲线
对应变换作用下得到曲线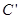 ,求曲线
,求曲线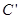 的方程.
的方程.
已知函数
(Ⅰ) 当 时, 求函数
时, 求函数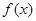 的单调增区间;
的单调增区间;
(Ⅱ) 求函数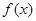 在区间
在区间 上的最小值;
上的最小值;
(Ⅲ) 设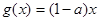 ,若存在
,若存在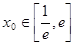 ,使得
,使得 成立,求实数
成立,求实数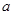 的取值范围.
的取值范围.
已知直线的极坐标方程为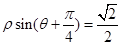 ,圆M的参数方程
,圆M的参数方程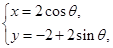 (其中
(其中 为参数)。
为参数)。
(1)将直线的极坐标方程化为直角坐标方程;
(2)求圆M上的点到直线的距离的最小值。