在直角坐标系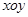 中,点
中,点 在矩阵
在矩阵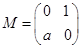 对应变换作用下得到点
对应变换作用下得到点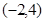 ,曲线
,曲线 在矩阵
在矩阵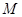 对应变换作用下得到曲线
对应变换作用下得到曲线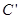 ,求曲线
,求曲线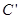 的方程.
的方程.
(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系 中,圆
中,圆 的参数方程为
的参数方程为 (
( 为参数).
为参数).
(1)以原点为极点、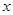 轴正半轴为极轴建立极坐标系,求圆
轴正半轴为极轴建立极坐标系,求圆 的极坐标方程;
的极坐标方程;
(2)已知 ,圆
,圆 上任意一点
上任意一点 ,求
,求 面积的最大值.
面积的最大值.
(本小题满分10分)选修4-1:几何证明选讲
如图所示, 为圆
为圆 的直径,
的直径, ,
,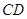 为圆
为圆 的切线,
的切线,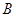 ,
, 为切点.
为切点.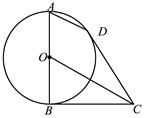
(1)求证: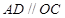 ;
;
(2)若圆 的半径为2,求
的半径为2,求 的值.
的值.
(本小题满分12分)定义在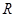 上的函数
上的函数 满足
满足 ,
, .
.
(1)求函数 的解析式;
的解析式;
(2)求函数 的单调区间;
的单调区间;
(3)如果 ,
, ,
, 满足
满足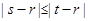 ,那么称
,那么称 比
比 更靠近
更靠近 .当
.当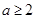 且
且 时,试比较
时,试比较 和
和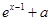 哪个更靠近
哪个更靠近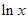 ,并说明理由.
,并说明理由.
(本小题满分12分)已知椭圆 :
: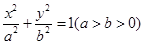 的上顶点为
的上顶点为 ,且离心率为
,且离心率为 .
.
(1)求椭圆 的方程;
的方程;
(2)证明:过椭圆 :
: 上一点
上一点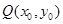 的切线方程为
的切线方程为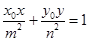 ;
;
(3)从圆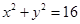 上一点
上一点 向椭圆
向椭圆 引两条切线,切点分别为
引两条切线,切点分别为 ,
, ,当直线
,当直线 分别与
分别与 轴,
轴, 轴交于
轴交于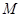 ,
, 两点时,求
两点时,求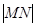 的最小值.
的最小值.
(本小题满分12分)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮训练,每人投10次,投中的次数统计如下表:
| 学生 |
1号 |
2号 |
3号 |
4号 |
5号 |
| 甲班 |
6 |
5 |
7 |
9 |
8 |
| 乙班 |
4 |
8 |
9 |
7 |
7 |
(1)从统计数据看,甲、乙两个班哪个班成绩更稳定(用数字特征说明);
(2)若把上表数据作为学生投篮命中率,规定两个班级的1号和2号同学分别代表自己的班级参加比赛,每人投篮一次,将甲、乙两个班两名同学投中的次数之和分别记作 和
和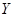 ,试求
,试求 和
和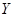 的分布列和数学期望.
的分布列和数学期望.