(本小题满分12分)
已知曲线C上任意一点M到点F(0,1)的距离比它到直线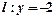 的距离小1.
的距离小1.
(1)求曲线C的方程;
(2)过点P(2,2)的直线与曲线C交于A、B两点,设 当△AOB的面积为
当△AOB的面积为 时(O为坐标原点),求的值.
时(O为坐标原点),求的值.
(3)若函数 在[1,3]上是减函数,求实数a的取值范围.
在[1,3]上是减函数,求实数a的取值范围.
((本小题满分15分)
已知圆C过定点F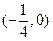 ,且与直线
,且与直线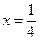 相切,圆心C的轨迹为E,曲线E与直线
相切,圆心C的轨迹为E,曲线E与直线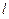 :
: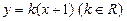 相
相 交于A、B两点。
交于A、B两点。
(I)求曲线E的方程;
(II)在曲线E上是否存在与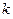 的取值无关的定点M,使得MA⊥MB?若存在,求出所有符合条件的定点M;若不存在,请说明理由。
的取值无关的定点M,使得MA⊥MB?若存在,求出所有符合条件的定点M;若不存在,请说明理由。
(本小题满分14分)已知函数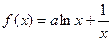
(1)当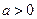 时,求函数
时,求函数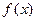 的单调区间和极值;
的单调区间和极值;
(2)当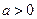 时,若
时,若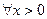 ,均有
,均有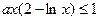 ,求实数
,求实数 的取值范围;
的取值范围;
(3)若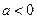 ,
,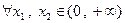 ,且
,且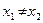 ,试比较
,试比较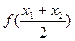 与
与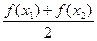 的大小.
的大小.
(本小题满分12分)
2010年推出一种新型家用轿车,购买时费用为14.4万元,每年应交付保险费.养路费及汽油费共0.7万元,汽车的维修费为:第一年无维修费用,第二年为0.2万元,从第三年起,每年的维修费均比上一年增加0.2万元.
(1)设该辆轿车使用n年的总费用(包括购买费用.保险费.养路费.汽油费及维修费)为f(n),求f(n)的表达式;
(2)这种汽车使用多少年报废最合算(即该车使用多少年,年平均费用最少)?
(本小题满分12分) 已知四棱锥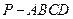 底面ABCD是矩形,PA⊥平面ABCD, AD=2,AB=1,E.F分别是线段AB.BC的中点,
底面ABCD是矩形,PA⊥平面ABCD, AD=2,AB=1,E.F分别是线段AB.BC的中点,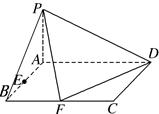
(1)证明:PF⊥FD;
(2)在PA上找一点G,使得EG∥平面PFD;.
(3)若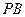 与平面
与平面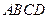 所成的角为
所成的角为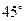 ,求二面角
,求二面角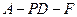 的余弦值.
的余弦值.
(本小题满分12分)
已知全集U = R,非空集合 ,
, .
.
(1)当 时,求(∁U
时,求(∁U )
) ;
;
(2)命题 ,命题
,命题 ,若
,若 是
是 的必要条件,求实数
的必要条件,求实数 的取值范围
的取值范围