小波以游戏方式决定是去打球、唱歌还是去下棋.游戏规则为:以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若X>0就去打球,若X=0就去唱歌,若X<0就去下棋.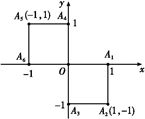
(1)写出数量积X的所有可能取值;
(2)分别求小波去下棋的概率和不去唱歌的概率.
有7位歌手(1至7号)参加一场歌唱比赛,由500名大众评委现场投票决定歌手名次.根据年龄将大众评委分为五组,各组的人数如下:
| 组别 |
A |
B |
C |
D |
E |
| 人数 |
50 |
100 |
150 |
150 |
50 |
(1)为了调查评委对7位歌手的支持状况,现用分层抽样方法从各组中抽取若干评委,其中从B组抽取了6人.请将其余各组抽取的人数填入下表.
| 组别 |
A |
B |
C |
D |
E |
| 人数 |
50 |
100 |
150 |
150 |
50 |
| 抽取人数 |
6 |
(2)在(1)中,若A,B两组被抽到的评委中各有2人支持1号歌手,现从这两组被抽到的评委中分别任选1人,求这2人都支持1号歌手的概率.
如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-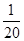 (1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.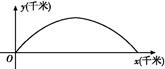
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标a不超过多少时,炮弹可以击中它?请说明理由.
如图,在直棱柱ABC A1B1C1中,∠BAC=90°,AB=AC=
A1B1C1中,∠BAC=90°,AB=AC=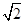 ,AA1=3,D是BC的中点,点E在棱BB1上运动.
,AA1=3,D是BC的中点,点E在棱BB1上运动.
(1)证明:AD⊥C1E;
(2)当异面直线AC,C1E所成的角为60°时,求三棱锥C1 A1B1E的体积.
A1B1E的体积.
如图,四棱柱ABCD A1B1C1D1的底面ABCD是正方形,O是底面中心,A1O⊥底面ABCD,AB=AA1=
A1B1C1D1的底面ABCD是正方形,O是底面中心,A1O⊥底面ABCD,AB=AA1=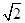 .
.
(1)证明:平面A1BD∥平面CD1B1;
(2)求三棱柱ABD A1B1D1的体积.
A1B1D1的体积.