如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在方程y=kx-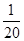 (1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1+k2)x2(k>0)表示的曲线上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.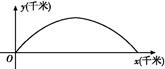
(1)求炮的最大射程;
(2)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标a不超过多少时,炮弹可以击中它?请说明理由.
(本小题满分12分)已知函数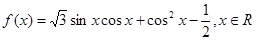
(1)求函数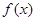 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(2)作出函数在一个周期内的图象。
已知二项式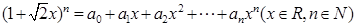
(1)若展开式中第五项的二项式系数是第三项系数的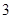 倍,求
倍,求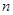 的值;
的值;
(2)若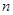 为正偶数时,求证:
为正偶数时,求证: 为奇数.
为奇数.
(3)证明: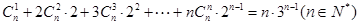
把正整数按从小到大顺序排列成下列数表,数表中第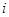 行共有
行共有 个正整数:
个正整数: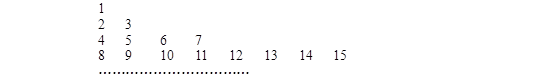
设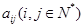 是位于数表中从上往下数第
是位于数表中从上往下数第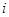 行、从左往右数第
行、从左往右数第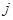 个数
个数
(1)若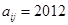 ,求
,求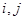 的值;
的值;
(2)记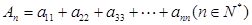 ,求数列
,求数列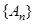 的通项公式;
的通项公式;
(3)猜想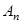 与
与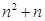 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
已知正方体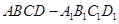 的棱长为1,点
的棱长为1,点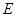 在
在 上,点
上,点 在
在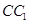 上,且
上,且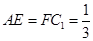
(1)求直线 与平面
与平面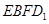 所成角的余弦值;
所成角的余弦值;
(2)用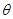 表示平面
表示平面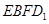 和侧面
和侧面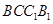 所成的锐二面角的大小,求
所成的锐二面角的大小,求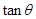 ;
;
(3)若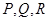 分别在
分别在 上,并满足
上,并满足 ,探索:当
,探索:当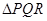 的重心为
的重心为 且
且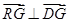 时,求实数
时,求实数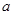 的取值范围.
的取值范围.
(1)试计算下列各式:(只需写出计算结果,不需写出计算过程)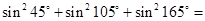 ____________
____________ ____________
____________ ____________
____________
(2)通过观察上述各式的计算规律,请你写出一般性的命题,并给出的证明
(参考公式: )
)