光明中学九（1）班的一个课外活动小组参加社会实践，他们到人民路口调查进入人民东路的车流量情况，下表是他们的调查记载表．
光明中学社会实践调查记载表
| 车辆类型 |
“正”字记录 |
辆数 |
占总车流量的百分比 |
| 公交车 |
正正正正正正 |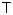
32 |
17.3% |
| 货车 |
正正正正正正正 |
39 |
21.1% |
| 小轿车 |
正正正正正正正正正正正正正正 |
74 |
 |
| 摩托车 |
正正正 |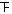
18 |
9.7% |
| 其他 |
正正正正 |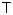
22 |
11.9% |
| 合计 |
|
185 |
100% |
请你根据表中数据，解答下列问题：表中有一处数据被墨汁污染，写出被污染处的数： %，并补全下面的车流量频数分布直方图；
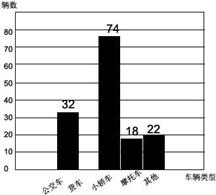
由经验估计可知，在所调查的时段内，每增加投放1辆公交车，可减少8辆小轿车．为了使该时段内，小轿车的流量减少到只比公交车多15辆，问公交公司应增加投放多少辆公交车？
已知：如图1，线段AB、CD相交于点O，连接AD、CB，我们把形如图1的图形称之为“8字形”．试解答下列问题：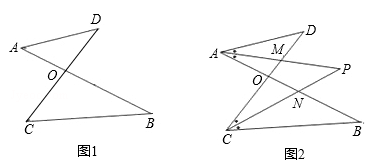
（1）在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关 ；
（2）在图2中，若∠D=40°，∠B=36°，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．利用（1）的结论，试求∠P的度数；
（3）如果图2中∠D和∠B为任意角时，其他条件不变，试问∠P与∠D、∠B之间存在着怎样的数量关系？并说明理由．
某商场计划购进A，B两种新型节能台灯共100盏，这两种台灯的进价、售价如表所示：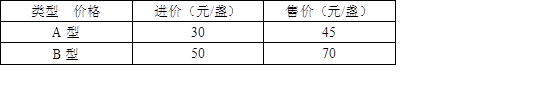
（1）设商场购进A型节能台灯为x盏，销售完这批台灯时可获利为y元，求y关于x的函数解析式；
（2）若商场规定B型台灯的进货数量不超过A型台灯数量的3倍，应怎样进货才能使商场在销售完这批台灯时获利最多？此时利润为多少元？
如图，△ABC中，∠A=30°，∠B=62°，CE平分∠ACB，CD⊥AB于D，DF⊥CE于F，求∠CDF的度数．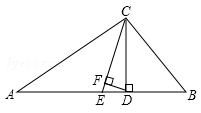
已知直线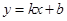
经过点A（5，0），B（1，4）．
（1）求直线AB的解析式；
（2）若直线
与直线AB相交于点C，求点C的坐标；
（3）根据图象，写出关于x的不等式
的解集．
如图，直角坐标系中，△ABC的顶点都在网格点上，其中，C点坐标为（1，2）．
（1）写出点A、B的坐标：A（ ， ）、B（ ， ）；
（2）将△ABC先向左平移2个单位长度，再向上平移1个单位长度，得到△A′B′C′，则A′B′C′的三个顶点坐标分别是A′（ ， ）、B′（ ， ）、C′（ ， ）；
（3）△ABC的面积为 ．