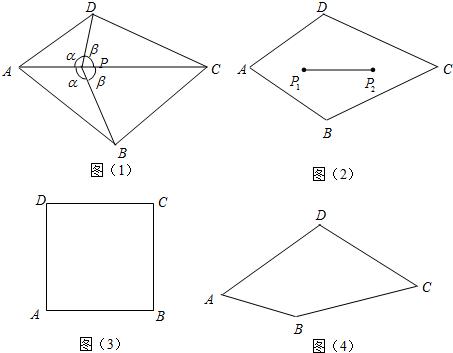
如图(1),凸四边形ABCD,如果点P满足∠APD=∠APB=α.且∠BPC=∠CPD=β,则称点P为四边形ABCD的一个半等角点.在图(3)正方形ABCD内画一个半等角点P,且满足α≠β;
在图(4)四边形ABCD中画出一个半等角点P,保留画图痕迹(不需写出画法);
若四边形ABCD有两个半等角点P1、P2(如图(2)),证明线段P1P2上任一点也是它的半等角点.
已知:如图,Rt△ABC中,∠A=900。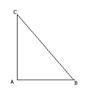
(1)求作:⊙O,使圆心在AC上,且与AB、BC相切;
(2)若∠B=600,AC= ,求⊙O的半径。
,求⊙O的半径。
先将下式化简,再选择一个你喜欢又使原式有意义的数代入求值。
为了求1+2+22+23+…+2100的值,可令S=1+2+22+23+…+2100,则2S=2+22+23+24+…+2101,因此2S﹣S=2101﹣1,所以S=2101﹣1,即1+2+22+23+…+2100=2101﹣1,仿照以上推理计算1+2+22+23+…+22014的值是
如图,在直角坐标系中,四边形OABC的OA,OC两边分别在x,y轴上,OA∥BC,BC=15cm,A点坐标为(16,0),C点坐标为(0,4).点P,Q分别从C,A同时出发,点P以2cm/s的速度由C向B运动,点Q以4cm/s的速度由A向O运动,当点Q到达点O时,点P也停止运动,设运动时间为t秒(0≤t≤4).
(1)求当t为多少时,四边形PQAB为平行四边形?
(2)求当t为多少时?PQ所在直线将四边形OABC分成左右两部分的面积比为1:2;
(3)直接写出在(2)的情况下,直线PQ的函数关系式.
如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(﹣4,0).
(1)求经过点C的反比例函数的解析式;
(2)设P是(1)中所求函数图象上一点,以P、O、A顶点的三角形的面积与△COD的面积相等.求点P的坐标.