在课外小组活动时，小伟拿来一道题（原问题）和小熊、小强交流.
原问题：如图1，已知△ABC, ∠ACB＝90°, ∠ABC＝45°，分别以AB、BC为边向外作△ABD与△BCE, 且DA＝DB, EB＝EC，∠ADB＝∠BEC＝90°，连接DE交AB于点F. 探究线段DF与EF的数量关系.小伟同学的思路是：过点D作DG⊥AB于G,构造全等三角形，通过推理使问题得解.小熊同学说:我做过一道类似的题目,不同的是∠ABC＝30°,∠ADB＝∠BEC＝60°.小强同学经过合情推理，提出一个猜想，我们可以把问题推广到一般情况.请你参考小慧同学的思路，探究并解决这三位同学提出的问题：写出原问题中DF与EF的数量关系
如图2，若∠ABC＝30°，∠ADB＝∠BEC＝60°，原问题中的其他条件不变，你在（1）中得到的结论是否发生变化？请写出你的猜想并加以证明；
如图3，若∠ADB＝∠BEC＝2∠ABC，原问题中的其他条件不变，你在（1）中
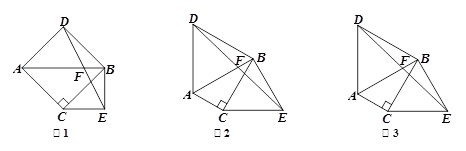
得到的结论是否发生变化？请写出你的猜想并加以证明
解方程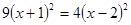
木匠黄师傅用长AB=3，宽BC=2的矩形木板做一个尽可能大的圆形桌面，他设计了四种方案：方案一：直接锯一个半径最大的圆；
方案二：圆心O1、O2分别在CD、AB上，半径分别是O1C、O2A，锯两个外切的半圆拼成一个圆；
方案三：沿对角线AC将矩形锯成两个三角形，适当平移三角形并锯一个最大的圆；
方案四：锯一块小矩形BCEF拼到矩形AFED下面，利用拼成的木板锯一个尽可能大的圆．
（1）写出方案一中圆的半径；
（2）通过计算说明方案二和方案三中，哪个圆的半径较大？
（3）在方案四中，设CE=x（0＜x＜1），圆的半径为y．
①求y关于x的函数解析式；
②当x取何值时圆的半径最大，最大半径为多少？并说明四种方案中哪一个圆形桌面的半径最大．
如图，Rt△ABC在平面直角坐标系中，BC在X轴上，B（﹣1，0）、A（0，2），AC⊥AB．
（1）求线段OC的长．
（2）点P从B点出发以每秒4个单位的速度沿x轴正半轴运动，点Q从A点出发沿线段AC以
个单位每秒速度向点C运 动，当一点停止运动，另一点也随之停止，设△CPQ的面 积为S，两点同时运动，运动的时间为t秒，求S与t之间关系式，并写出自变量取值范围．
（3）Q点沿射线AC按原速度运动，⊙G过A、B、Q三点，是否有这样的t值使点P在⊙G上、如果有求t值，如果没有说明理由．
（1）问题发现
如图1，△ACB和△DCE均为等边三角形，点A、D、E在同一直线上，连接BE，
填空：①∠AEB的度数为；
②线段AD、BE之间的数量关系是．
（2）拓展探究
如图2，△ACB和△DCE均为等腰直角三角形，∠ACB=∠DCE=900， 点A、D、E在同一直线上，CM为△DCE中DE边上的高，连接BE．请判断∠AEB的度数及线段CM、AE、BE之间的数量关系，并说明理由．
（3）解决问题如图3，在正方形ABCD中，CD=
．若点P满足PD=1，且∠BPD=900，请直接写出点A到BP的距离．
国家限购以来，二手房和新楼盘的成交量迅速下降．据统计，无锡在限购前某季度二手房和新楼盘成交量为9500套．限购后，同一季度二手房和新楼盘的成交量共4425套．其中二手房成交量比限购前减少55﹪，新楼盘成交量比限购前减少52﹪．
（1）问限购后二手房和新楼盘各成交多少套？
（2）在成交量下跌的同时，房价也大幅跳水．某楼盘限购前均价为12000元/m，限购后，无人问津，房价进行调整，二次下调后均价为7680元/m，求平均每次下调的百分率？总理表态：让房价回归合理价位．合理价位为房价是可支配收入的3～6倍，假设无锡平均每户家庭（三口之家）的年可支配收入为9万元，每户家庭的平均住房面积为80 m，问下调后的房价回到合理价位了吗？请说明理由．