如图(a),小球甲固定于水平气垫导轨的左端,质量m=0.4kg的小球乙可在导轨上无摩擦地滑动,甲、乙两球之间因受到相互作用而具有一定的势能,相互作用力沿二者连线且随间距的变化而变化。现已测出势能随位置x的变化规律如图(b)中的实线所示。已知曲线最低点的横坐标x0=20cm,虚线①为势能变化曲线的渐近线,虚线②为经过曲线上某点的切线。
(1)将小球乙从x1=8cm处由静止释放,小球乙所能达到的最大速度为多大?
(2)假定导轨右侧足够长,将小球乙在导轨上从何处由静止释放,小球乙不可能第二次经过x0=20cm的位置?并写出必要的推断说明;
(3)若将导轨右端抬高,使其与水平面的夹角α=30°,如图(c)所示。将球乙从x2=6cm处由静止释放,小球乙运动到何处时速度最大?并求其最大速度;
(4)在图(b)上画出第(3)问中小球乙的动能Ek与位置x的关系图线。

如图所示,在直角坐标系xoy的第一、四象限区域内存在两个有界的匀强磁场:垂直纸面向外的匀强磁场I以及匀强磁场Ⅱ,O、M、P、Q为磁场边界和x轴的交点,MP区域是真空的,OM=MP=L。在第二象限存在沿x轴正向的匀强电场.一质量为m带电量为+q的带电粒子从电场中坐标为(-L,O)的点以速度v0沿+y方向射出,从y轴上坐标(O,2L) 的C处射入区域I,并且沿x的正方向射出区域I,带电粒子经过匀强磁场Ⅱ后第二次经过y,轴时就回到C点(粒子的重力忽略不计).求:
(1)第二象限匀强电场场强E的大小;
(2)区域I内匀强磁场磁感应强度B的大小;
(3)问区域Ⅱ内磁场的宽度至少为多少?
(4)粒子两次经过C的时间间隔为多少?
(5)请你通过对粒子运动轨迹描述定性判断:带电粒子能否通过坐标为(L,10L)的点.
如图所示AB为半径R=1m四分之一光滑绝缘竖直圆弧轨道,在四分之一圆弧区域内存在着E=1× V/m竖直向上的匀强电场,有一质量m=lkg带电量q=1.4×
V/m竖直向上的匀强电场,有一质量m=lkg带电量q=1.4× C正电荷的物体(可视为质点),从A点的正上方距离A点H处由静止开始自由下落(不计空气阻力),BC段为长L=2m,与物体动摩擦因素
C正电荷的物体(可视为质点),从A点的正上方距离A点H处由静止开始自由下落(不计空气阻力),BC段为长L=2m,与物体动摩擦因素 =0.2的粗糙绝缘水平面,CD段为倾角
=0.2的粗糙绝缘水平面,CD段为倾角 =
= 且离地面DE高h=0.8m的斜面。求:
且离地面DE高h=0.8m的斜面。求:
(1)若H=1m,物体能沿轨道AB到达最低点曰,求它到达B点时对轨道的压力大小?
(2)通过你的计算判断:是否存在某一H值,能使物体沿轨道AB经过最低点B后最终停在距离B点0.8m处?
(3)若高度H满足: ,请通过计算标示出物体从C处射出后打到的范围。(已知
,请通过计算标示出物体从C处射出后打到的范围。(已知 。不需要计算过程,但要具体的位置。不讨论物体的反弹以后的情况。)
。不需要计算过程,但要具体的位置。不讨论物体的反弹以后的情况。)
轻质细线吊着一质量为m=0.42kg,边长为L=1m、匝数n=10的正方形线圈,其总电阻为r=l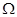 。在框的中间位置以下区域分布着矩形磁场,如图甲所示.磁场方向垂直纸面向里,大小随时间变化如图乙所示,
。在框的中间位置以下区域分布着矩形磁场,如图甲所示.磁场方向垂直纸面向里,大小随时间变化如图乙所示,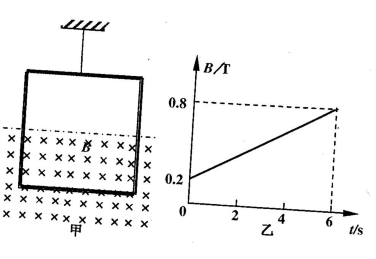
求:
(1)判断线圈中产生的感应电流的方向是顺时针还是逆时针?
(2)线圈的电功率;
(3)在t=4s时轻质细线的拉力大小
在某一旅游景区,建有一山坡滑草运动项目,已知山坡是倾角为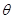 =300的倾斜直轨道。一名游客连同滑草装置质量为m=80kg从静止开始匀加速下滑,在时间t=5s内沿斜面滑下的位移x="50" m(不计空气阻力).求:
=300的倾斜直轨道。一名游客连同滑草装置质量为m=80kg从静止开始匀加速下滑,在时间t=5s内沿斜面滑下的位移x="50" m(不计空气阻力).求:
(1)该游客下滑过程中的加速度多大?
(2)滑草装置与草皮之间的动摩擦因数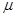 为多大?
为多大?
(3)设游客滑下50 m后进入水平草坪,则游客在水平草坪上滑动的最大距离是多少?(假设滑草装置与水平面、斜面的动摩擦因素相同,且进入水平轨道的瞬间速度大小不变)
如图甲所示,M、N为水平放置的平行板电容器的两个极板,两极板间距d=0.1m,两极板间的电压U=12.5V,O为上极板中心的小孔,以O为坐标原点,在竖直平面内建立直角坐标系,在y轴方向上,0≤y≤2m区间存在方向与x轴平行的匀强电场(PQ为电场区域的上边界),在x轴方向上,电场范围足够大。若规定x轴正方向为电场正方向,电场强度随时间变化情况如图乙所示。现有一个带负电的粒子,在t=0时刻从紧靠M级板中心O'处无初速释放,经过小孔O进入N板上方的交变电场中,粒子的比荷q/m=1×102C/kg,不计粒子重力。求: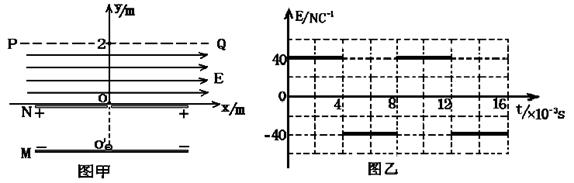
(1)粒子进入交变电场时的速度。
(2)粒子在两板之间飞行的时间。
(3)粒子在8×10-3s末的位置坐标。
(4)粒子离开交变电场时的速度大小和方向。