在直三棱柱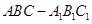 中,
中,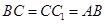 ="2" ,
="2" ,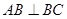 .点
.点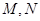 分别是
分别是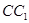 ,
,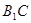 的中点,
的中点,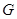 是棱
是棱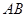 上的动点.
上的动点.
(I)求证: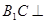 平面
平面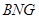 ;
;
(II)若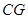 //平面
//平面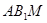 ,试确定
,试确定 点的位置,
点的位置,
并给出证明;
(III)求二面角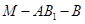 的余弦值.
的余弦值.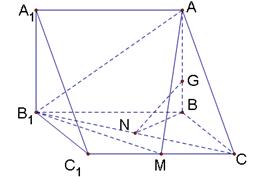 【
【
如图所示,AB是☉O的直径,弦BD、CA的延长线相交于点E,F为BA延长线上一点,且BD·BE=BA·BF,求证: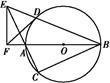
(1)EF⊥FB;
(2)∠DFB+∠DBC=90°.
如图所示,已知C点在圆O直径BE的延长线上,CA切圆O于A点,∠ACB的平分线CD交AE于点F,交AB于点D.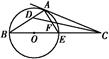
(1)求∠ADF的度数;
(2)若AB=AC,求AC∶BC.
如图所示,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合.已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x+mn=0的两个根.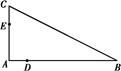
(1)证明:C,B,D,E四点共圆;
(2)若∠A=90°,且m=4,n=6,求C,B,D,E所在圆的半径.
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E、F分别为弦AB与弦AC上的点,且BC·AE=DC·AF,B、E、F、C四点共圆.
(1)证明:CA是△ABC外接圆的直径;
(2)若DB=BE=EA,求过B、E、F、C四点的圆的面积与△ABC外接圆面积的比值.
如图所示,AB为☉O直径,直线CD与☉O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.证明: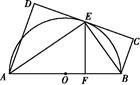
(1)∠FEB=∠CEB;
(2)EF2=AD·BC.