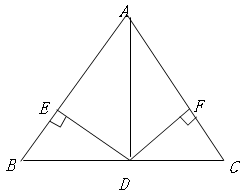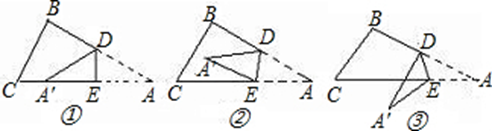
如图①,一张三角形ABC纸片,点D、E分别是△ABC边上两点.
研究(1):如果沿直线DE折叠,使A点落在CE上,则∠BDA′与∠A的数量关系是__ ▲_________
∠BDA′=2∠A
∠BDA′+∠CEA′=2∠A如果折成图②的形状,猜想∠BDA′、∠CEA和∠A的数量关系是__ ▲_________
如果折成图③的形状,猜想∠BDA′、∠CEA′和∠A的数量关系,并说明理由.
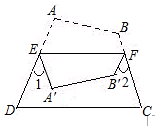
猜想:▲________将问题1推广,如图,将四边形ABCD纸片沿EF折叠,使点A、B落在四边形EFCD的内部时,∠1+∠2与∠A、∠B之间的数量关系是_ ▲________
已知:如图①,在 中,
中,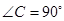 ,
,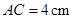 ,
,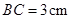 ,点
,点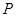 由
由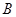 出发沿
出发沿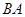 方向向点
方向向点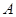 匀速运动,速度为1cm/s;点
匀速运动,速度为1cm/s;点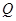 由
由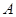 出发沿
出发沿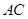 方向向点
方向向点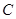 匀
匀
速运动,速度为2cm/s;连接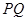 .若设运动的时间为
.若设运动的时间为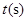 (
(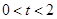 ),解答下列问题:
),解答下列问题:
(1)当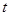 为何值时,
为何值时,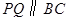 ?
?
(2)设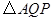 的面积为
的面积为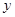 (
(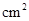 ),求
),求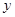 与
与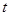 之间的函数关系式;
之间的函数关系式;
(3)是否存在某一时刻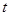 ,使线段
,使线段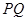 恰好把
恰好把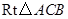 的周长和面积同时平分?若存在,求出此时
的周长和面积同时平分?若存在,求出此时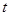 的值;若不存在,说明理由;
的值;若不存在,说明理由;
(4)如图②,连接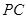 ,并把
,并把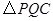 沿
沿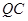 翻折,得到四边形
翻折,得到四边形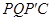 ,那么是否存在某一时刻
,那么是否存在某一时刻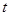 ,使四边形
,使四边形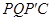 为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.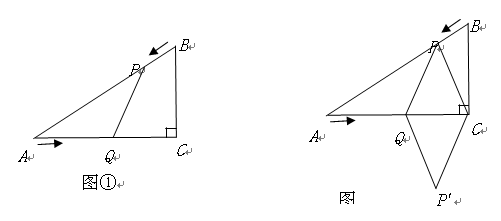
在△ABD中,E、H分别是AB、AD的中点,则EH∥BD,
同理GH∥AC,如图,梯形ABCD中,AD//BC,AB=CD,对角线AC、BD交于点O,AC BD,E、F、G、H分别为AB、BC、CD、DA的中点.
BD,E、F、G、H分别为AB、BC、CD、DA的中点.
(1)求证:四边形EFGH为正方形;
(2)若AD=4,BC=6,求四边形EFGH的面积.
在△ABD中,E、H分别是AB、AD的中点,
则EH∥BD,
同理GH∥AC,如图,梯形ABCD中,AD//BC,AB=CD,对角线AC、BD交于点O,AC BD,E、F、G、H分别为AB、BC、CD、DA的中点.
BD,E、F、G、H分别为AB、BC、CD、DA的中点.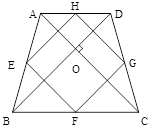
(1)求证:四边形EFGH为正方形;
(2)若AD=4,BC=6,求四边形EFGH的面积.
如图,DB∥AC,且DB=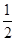 AC,E是AC的中点,
AC,E是AC的中点,
(1)求证:BC=DE;
(2)连结AD、BE,若要使四边形DBEA是矩形,则给△ABC添加一个什么条件,为什么?
(3)在(2)的条件下,若要使四边形DBEA是正方形,则∠C=0.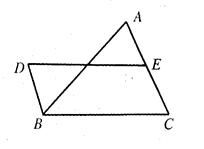
如图:已知在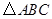 中,AD平分∠BAC,
中,AD平分∠BAC,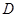 为
为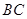 边的中点,过点
边的中点,过点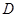 作
作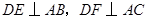 ,垂足分别为
,垂足分别为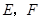 。
。
(1)求证: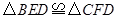 ;
;
(2)若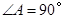 ,求证:四边形
,求证:四边形 是正方形。
是正方形。