如图1,在平面直角坐标系中,以坐标原点O为圆心的⊙O的半径为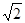
－1,直线l y=－X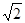－与坐标轴分别交于A,C两点,点B的坐标为(4,1) ,⊙B与X轴相切于点M.
(1) 求点A的坐标及∠CAO的度数;
(2) ⊙B以每秒1个单位长度的速度沿X轴负方向平移,同时,直线l绕点A顺时针匀速旋转.当⊙B第一次与⊙O相切时,直线l也恰好与⊙B第一次相切.问:直线AC绕点A每秒旋转多少度?
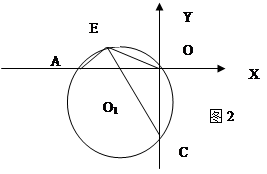
(3)如图2.过A,O,C三点作⊙O1 ,点E是劣弧
上一点,连接EC,EA.EO,当点E在劣弧上运动时(不与A,O两点重合),
的值是否发生变化?如果不变,求其值,如果变化,说明理由.
.
“惠民”经销店为某工厂代销一种工业原料（代销是指厂家先免费提供货源，待货物售出后再进行结算，未售出的由厂家负责处理）．当每吨售价为260元时，月销售量为45吨；该经销店为提高经营利润，准备采取降价的方式进行促销，经市场调查发现：当每吨售价每下降10元时，月销售量就会增加7.5吨．综合考虑各种因素，每售出一吨工业原料共需支付厂家及其它费用100元．
（1）当每吨售价是240元时，计算此时的月销售量；
（2）若在“薄利多销、让利于民”的原则下，当每吨原料售价为多少时，该店的月利润为9000元；
（3）每吨原料售价为多少时，该店的月利润最大，求出最大利润．
如图，点E、F分别是
ABCD的边BC、AD上的点，且BE=DF．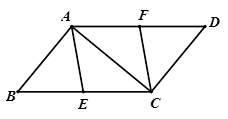
（1）求证：四边形AECF是平行四边形；
（2）若AE=BE，∠BAC＝90°，试判断四边形AECF的形状，并说明理由．
某中学开展“中国梦、我的梦”演讲比赛，甲、乙两班根据初赛成绩各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示．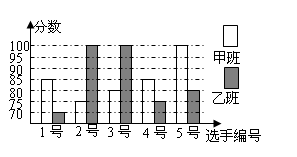
（1）根据下图，分别求出两班复赛的平均成绩和方差；
（2）根据（1）的计算结果，分析哪个班级的复赛成绩较好？
已知关于x的方程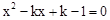
．
（1）求证：无论k取什么实数值，这个方程总有实数根；
（2）当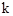
=3时，△ABC的每条边长恰好都是方程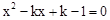的根，求△ABC的周长．
当a=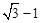
时，求
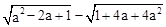的值．