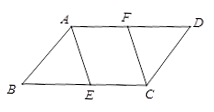甲、乙两辆汽车同时分别从 、
、 两城沿同一条高速公路匀速驶向
两城沿同一条高速公路匀速驶向 城.已知
城.已知 、
、 两城的距离为450千米,
两城的距离为450千米,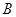 、
、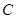 两城的距离为400千米,乙车比甲车的速度每小时慢10千米,结果两辆车同时到达
两城的距离为400千米,乙车比甲车的速度每小时慢10千米,结果两辆车同时到达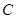 城.设甲车的速度为每小时
城.设甲车的速度为每小时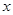 千米.
千米.
(1)根据题意填写下表(用含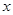 的代数式表示):
的代数式表示):
| 行驶的路程(千米) |
速度(千米/时) |
所需时间(小时) |
|
| 甲车 |
450 |
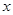 |
|
| 乙车 |
400 |
(2)求甲、乙两车的速度.
如图,四边形 为正方形,点
为正方形,点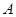 在
在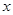 轴上,点
轴上,点 在
在 轴上,且
轴上,且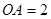 ,
,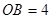 ,反比例函数
,反比例函数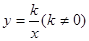 在第一象限的图像经过正方形的顶点
在第一象限的图像经过正方形的顶点 .
.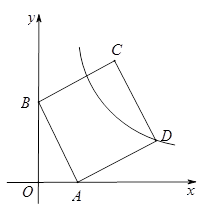
(1)求反比例函数的关系式;
(2)将正方形 沿
沿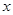 轴向左平移个单位长度时,点
轴向左平移个单位长度时,点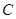 恰好落在反比例函数的图像上.
恰好落在反比例函数的图像上.
某中学为了了解七年级男生入学时的跳绳情况,随机选取50名刚入学的男生进行个人一分钟跳绳测试,并以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图(如图所示).

根据图表解答下列问题:
(1)在统计表中,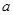 的值为,
的值为,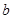 的值为,并将统计图补充完整(温馨提示:作图时别忘了用黑色签字笔涂黑);
的值为,并将统计图补充完整(温馨提示:作图时别忘了用黑色签字笔涂黑);
(2)这个样本数据的中位数落在第组;
(3)若七年级男生个人一分钟跳绳次数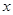 ≥130时成绩为优秀,该校七年级入学时男生共有150人,请估计该校七年级男生个人一分钟跳绳成绩为优秀的人数.
≥130时成绩为优秀,该校七年级入学时男生共有150人,请估计该校七年级男生个人一分钟跳绳成绩为优秀的人数.
一个盒子中装有4张形状大小都相同的卡片,卡片上的编号分别为1、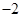 、
、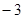 、
、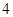 ,现从盒子中随机抽取一张卡片,将其编号记为
,现从盒子中随机抽取一张卡片,将其编号记为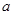 ,再从剩下的三张中任取一张,将其编号记为
,再从剩下的三张中任取一张,将其编号记为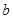 ,这样就确定了点
,这样就确定了点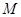 的一个坐标,记为
的一个坐标,记为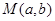 .
.
(1)求第一次抽到编号为 的概率;
的概率;
(2)请用树状图或列表法,求点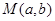 在第四象限的概率.
在第四象限的概率.
如图,在□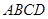 中,点
中,点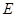 、
、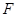 分别是
分别是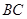 、
、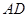 的中点.求证:
的中点.求证: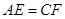 .
.