探究
在图1中，已知线段AB，CD，其中点分别为E，F．
①若A (-1，0)， B (3，0)，则E点坐标为__________；
②若C (-2，2)， D (-2，-1)，则F点坐标为__________；
归纳
①在图2中，已知线段AB的端点坐标为A(1，1) ，B(3，3)，
则AB 的中点C的坐标__________
②无论线段AB处于直角坐标系中的哪个位置，当其端点坐标为
A(a，b)，B(c，d)， AB中点C的坐标为______ 
运用
在图3中，一次函数
与反比例函数
的图象交点为A（-1，-3），B（3 , n）．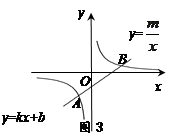
①求出m、n的值；
②求出一次函数的表达式；
③若四边形AOBP为平行四边形,请利用上面的结论求出顶点P的坐标．
在重阳节敬老爱老活动中，某校计划组织志愿者服务小组到“夕阳红”敬老院为老人服务，准备从初三（1）班中的3名男生小亮、小明、小伟和2名女生小丽、小敏中选取一名男生和一名女生参加学校志愿者服务小组．
（1）若随机选取一名男生和一名女生参加志愿者服务小组，请用树状图或列表法写出所有可能出现的结果；
（2）求出恰好选中男生小明与女生小丽的概率．
如图，在矩形ABCD中，E，F为BC上两点，且BE=CF，连接AF，DE交于点O．求证：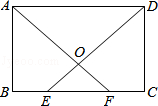
（1）△ABF≌△DCE；
（2）△AOD是等腰三角形．
直线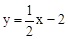
与x、y轴分别交于点A、C．抛物线的图象经过A、C和点B（1，0）．
（1）求抛物线的解析式；
（2）在直线AC上方的抛物线上有一动点D，当D与直线AC的距离DE最大时，求出点D的坐标，并求出最大距离是多少？
已知：⊙O的直径为3，线段AC=4，直线AC和PM分别与⊙O相切于点A，M．
（1）求证：点P是线段AC的中点；
（2）求sin∠PMC的值．
某校为了丰富学生的校园生活，准备购进一批篮球和足球．其中篮球的单价比足球的单价多40元，用1500元购进的篮球个数与900元购进的足球个数相等．
（1）篮球和足球的单价各是多少元？
（2）该校打算用1000元购买篮球和足球，问恰好用完1000元，并且篮球、足球都买有的购买方案有哪几种？