直线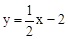 与x、y轴分别交于点A、C.抛物线的图象经过A、C和点B(1,0).
与x、y轴分别交于点A、C.抛物线的图象经过A、C和点B(1,0).
(1)求抛物线的解析式;
(2)在直线AC上方的抛物线上有一动点D,当D与直线AC的距离DE最大时,求出点D的坐标,并求出最大距离是多少?
已知:如图, ,射线 上一点 .
求作:等腰 ,使线段 为等腰 的底边,点 在 内部,且点 到 两边的距离相等.

如图,在平面直角坐标系中, , , ,点 的坐标为 .抛物线 经过 、 两点.
(1)求抛物线的解析式;
(2)点 是直线 上方抛物线上的一点,过点 作 垂直 轴于点 ,交线段 于点 ,使 .
①求点 的坐标;
②在直线 上是否存在点 ,使 为直角三角形?若存在,求出符合条件的所有点 的坐标;若不存在,请说明理由.

将矩形 绕点 顺时针旋转 ,得到矩形 .

(1)如图,当点 在 上时.求证: ;
(2)当 为何值时, ?画出图形,并说明理由.
甲、乙两人分别从 , 两地同时出发,匀速相向而行.甲的速度大于乙的速度,甲到达 地后,乙继续前行.设出发 后,两人相距 ,图中折线表示从两人出发至乙到达 地的过程中 与 之间的函数关系.
根据图中信息,求:
(1)点 的坐标,并说明它的实际意义;
(2)甲、乙两人的速度.

如图, 为等腰三角形, 是底边 的中点,腰 与 相切于点 , 与 相交于点 .
(1)求证: 是 的切线;
(2)若 , .求阴影部分的面积.
