已知:矩形纸片ABCD中,AB=26厘米,BC=18.5厘米,点E在AD上,且AE=6厘米,点P是AB边上一动点.按如下操作:
步骤一,折叠纸片,使点P与点E重合,展开纸片得折痕MN(如图1所示);
步骤二,过点P作PT⊥AB,交MN所在的直线于点Q,连接QE(如图2所示)无论点P在AB边上任何位置,都有PQ_________QE(填“
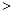 ”、“
”、“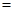 ”、“
”、“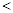 ”号);
”号);如图3所示,将纸片ABCD放在直角坐标系中,按上述步骤一、二进行操作:
①当点P在A点时,PT与MN交于点Q1,Q1点的坐标是(_______,_________);
②当PA=6厘米时,PT与MN交于点Q2. Q2点的坐标是(_______,_________);
③当PA=12厘米时,在图3中画出MN,PT(不要求写画法),并求出MN与PT的交点Q3的坐标;点P在运动过程,PT与MN形成一系列的交点Q1,Q2,Q3……观察、猜想:众多的交点形成的图象是什么?并直接写出该图象的函数表达式.
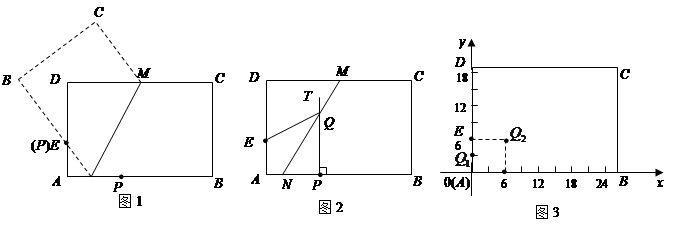
某冰箱厂为响应国家“家电下乡”号召,计划生产A、B两种型号的冰箱100台.经预算,两种冰箱全部售出后,可获得利润不低于4.75万元,不高于4.8万元,两种型号的冰箱生产成本和售价如下表:
| 型号 |
A型 |
B型 |
| 成本(元/台) |
2200 |
2600 |
| 售价(元/台) |
2800 |
3000 |
(1)冰箱厂有哪几种生产方案?
(2)该冰箱厂按哪种方案生产,才能使投入成本最少?“家电下乡 ”后农民买家电(冰箱、彩电、洗衣
”后农民买家电(冰箱、彩电、洗衣 机)可享受13%的政府补贴,那么在这种方案下政府需补贴给农民多少元?
机)可享受13%的政府补贴,那么在这种方案下政府需补贴给农民多少元?
将一袋桔子分给若干个儿童,如果每人分4个桔子,则剩下9个桔子;如果每人分6 个桔子,则最后一个儿童分得的桔子数将少于3个,求儿童人数和桔子的个数
今年7月我校修理操场,准备用载重4吨和2.5吨的汽车一次运走40吨的渣土,已知载重4吨的汽车比载重2.5吨的汽车少3辆,求这两种汽车各有多少辆?
如图,∠AOB=100°,OF是∠BOC的平分线,∠AOE=∠EOD,∠EOF=140°,求:∠COD的度数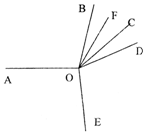
已知线段AB=20cm,在直线AB上有一点C,BC=4cm,P为线段AC中点,求线段BP的长