在直角坐标系 中,点p到两点
中,点p到两点 的距离之和等于4,
的距离之和等于4,
设点P的轨迹为C,直线 与C交于A、B两点,
与C交于A、B两点,
(1)写出C的方程;
(2)若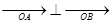 ,求k的值。
,求k的值。
如图,在直三棱柱ABC--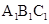 中,AC=3,BC=4,AB=5,
中,AC=3,BC=4,AB=5, ,点D是AB的中点。
,点D是AB的中点。
(1)求证: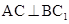 ;
;
(2)求证: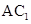 ∥平面
∥平面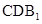
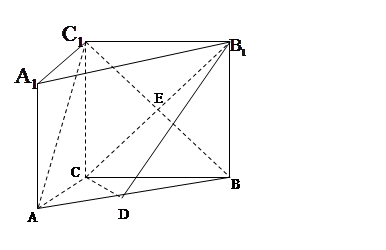
通过市场调查,得到某产品的资金投入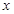 (万元)与获得的利润
(万元)与获得的利润 (万元)的数据,如下表所示:
(万元)的数据,如下表所示:
(1)画出数据对应的散点图;
(2)根据上表提供的数据,用最小二乘法求线性回归直线方程 ;
;
(3)现投入资金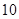 (万元),求估计获得的利润为多少万元.
(万元),求估计获得的利润为多少万元.
已知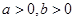 ,求证:
,求证: ≥
≥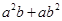 .
.
某高校“统计初步”课程教师随机调查了选该课的一些学生情况,共调查了50人,其中女生27人,男生23人。女生中有20人选统计专业。另外7人选非统计专业;男生中中有10人统计专业,另外,13人选非统计专业。
(1)根据以上数据完成下列的2×2列联表
| 专业 性别 |
非统计专业 |
统计专业 |
总计 |
| 男 |
|||
| 女 |
|||
| 总计 |
(2)根据以上数据,能否在犯错误的概率不超过0.05的前提下,认为主修统计专业与性别有关系?
实数m取什么数值时,复数 分别是:
分别是:
(1)实数? (2)虚数?