已知函数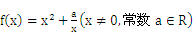
(1)判断函数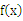
的奇偶性，并说明理由；
(2) 若函数数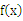在区间
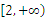上是增函数，求实数a的取值范围。
已知算法：
S1输入x；
S2若x＜0，执行S3,否则，执行S6；
S3 y=x+1；
S4输出y；
S5结束；
S6若x=0，执行S7,否则执行S10；
S7 y=0；
S8输出y；
S9结束；
S10 y=x；
S11输出y；
S12结束.
将该算法用程序框图来描述.
函数y=
写出求该函数值的算法及程序框图.
如图，该框图实现的是求方程ax+b=0(a、b为常数)的解. 
问：该框图正确吗？若不正确，请问它是哪一个问题的程序框图？应怎样修改？写出正确的算法及程序框图.
画出求a,b中的较大数的程序框图.
下表提供了一种二进制与十六进制之间的转换方法,这也是实际使用的方法之一,利用这个对照表,十六进制与二进制之间就可以实现逐段转换了.求十六进制的C7A16转化为二进制数的算法.
| 二进制 |
000 |
0001 |
0010 |
0011 |
0100 |
0101 |
0110 |
0111 |
| 十六进制 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 二进制 |
1000 |
1001 |
1010 |
1011 |
1100 |
1101 |
1110 |
1111 |
| 十六进制 |
8 |
9 |
A |
B |
C |
D |
E |
F |